
【題目】如圖12,已知拋物線![]() 過點
過點![]() ,
,![]() ,過定點
,過定點![]() 的直線
的直線![]() 與拋物線交于
與拋物線交于![]() ,
,![]() 兩點,點
兩點,點![]() 在點
在點![]() 的右側,過點
的右側,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() .
.
(1)求拋物線的解析式;
(2)當點![]() 在拋物線上運動時,判斷線段
在拋物線上運動時,判斷線段![]() 與
與![]() 的數(shù)量關系(
的數(shù)量關系(![]() 、
、![]() 、
、![]() ),并證明你的判斷;
),并證明你的判斷;
(3)![]() 為
為![]() 軸上一點,以
軸上一點,以![]() 為頂點的四邊形是菱形,設點
為頂點的四邊形是菱形,設點![]() ,求自然數(shù)
,求自然數(shù)![]() 的值;
的值;
(4)若![]() ,在直線
,在直線![]() 下方的拋物線上是否存在點
下方的拋物線上是否存在點![]() ,使得
,使得![]() 的面積最大,若存在,求出點
的面積最大,若存在,求出點![]() 的坐標及
的坐標及![]() 的最大面積,若不存在,請說明理由.
的最大面積,若不存在,請說明理由. 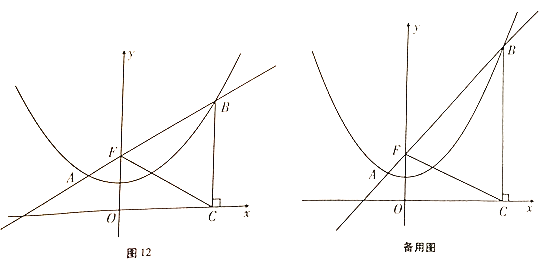
【答案】(1)y=![]() x2+1;(2)BF=BC,理由詳見解析;(3)6;(4)當t=2時,S△QBF有最大值,最大值為
x2+1;(2)BF=BC,理由詳見解析;(3)6;(4)當t=2時,S△QBF有最大值,最大值為![]() +1,此時Q點坐標為(2,2).
+1,此時Q點坐標為(2,2).
【解析】試題分析:(1)利用待定系數(shù)法求拋物線解析式;(2)設B(x, x2+1),而F(0,2),利用兩點間的距離公式得到BF2=x2+(x2+1﹣2)2=,再利用配方法可得到BF=x2+1,由于BC=x2+1,所以BF=BC;(3)如圖1,利用菱形的性質得到CB=CF=PF,加上CB=FB,則可判斷△BCF為等邊三角形,所以∠BCF=60°,則∠OCF=30°,于是可計算出CF=4,所以PF=CF=4,從而得到自然數(shù)m的值為6;(4)作QE∥y軸交AB于E,如圖2,先解方程組得B(1+![]() ,3+
,3+![]() ),設Q(t,
),設Q(t,![]() t2+1),則E(t,t+2),則EQ=﹣
t2+1),則E(t,t+2),則EQ=﹣![]() t2+t+1,則S△QBF=S△EQF+S△EQB=
t2+t+1,則S△QBF=S△EQF+S△EQB=![]() (1+
(1+![]() )EQ=
)EQ=![]() (1+
(1+![]() ))(﹣
))(﹣![]() t2+t+1),然后根據(jù)二次函數(shù)的性質解決問題.
t2+t+1),然后根據(jù)二次函數(shù)的性質解決問題.
試題解析:
(1)把點(﹣2,2),(4,5)代入y=ax2+c得![]() ,解得
,解得![]() ,
,
所以拋物線解析式為y=![]() x2+1;
x2+1;
(2)BF=BC.
理由如下:
設B(x,![]() x2+1),而F(0,2),
x2+1),而F(0,2),
∴BF2=x2+(![]() x2+1﹣2)2=x2+(
x2+1﹣2)2=x2+(![]() x2﹣1)2=(
x2﹣1)2=(![]() x2+1)2,
x2+1)2,
∴BF=![]() x2+1,
x2+1,
∵BC⊥x軸,
∴BC=![]() x2+1,
x2+1,
∴BF=BC;
(3)如圖1,m為自然數(shù),則點P在F點上方,
∵以B、C、F、P為頂點的四邊形是菱形,
∴CB=CF=PF,
而CB=FB,
∴BC=CF=BF,
∴△BCF為等邊三角形,
∴∠BCF=60°,
∴∠OCF=30°,/span>
在Rt△OCF中,CF=2OF=4,
∴PF=CF=4,
∴P(0,6),
即自然數(shù)m的值為6;
(4)作QE∥y軸交AB于E,如圖2,
當k=1時,一次函數(shù)解析式為y=x+2,
解方程組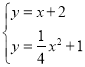 得
得 或
或 ,則B(1+
,則B(1+![]() ,3+
,3+![]() ),
),
設Q(t,![]() t2+1),則E(t,t+2),
t2+1),則E(t,t+2),
∴EQ=t+2﹣(![]() t2+1)=﹣
t2+1)=﹣![]() t2+t+1,
t2+t+1,
∴S△QBF=S△EQF+S△EQB=![]() (1+
(1+![]() )EQ=
)EQ=![]() (1+
(1+![]() ))(﹣
))(﹣![]() t2+t+1)=﹣
t2+t+1)=﹣![]() (t﹣2)2+
(t﹣2)2+![]() +1,
+1,
當t=2時,S△QBF有最大值,最大值為![]() +1,此時Q點坐標為(2,2).
+1,此時Q點坐標為(2,2).


 快樂5加2金卷系列答案
快樂5加2金卷系列答案科目:初中數(shù)學 來源: 題型:
【題目】已知等腰三角形其中一個內角為70°,那么這個等腰三角形的頂角度數(shù)為( )
A. 70° B. 70°或55° C. 40°或55° D. 70°或40°
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某校決定加強羽毛球、籃球、乒乓球、排球、足球五項球類運動,每位同學必須且只能選擇一項球類運動,對該校學生隨機抽取![]() 進行調查,根據(jù)調查結果繪制了如下不完整的頻數(shù)分布表和扇形統(tǒng)計圖:
進行調查,根據(jù)調查結果繪制了如下不完整的頻數(shù)分布表和扇形統(tǒng)計圖:
運動項目 | 頻數(shù)(人數(shù)) |
羽毛球 | 30 |
籃球 |
|
乒乓球 | 36 |
排球 |
|
足球 | 12 |

請根據(jù)以上圖表信息解答下列問題:
(1)頻數(shù)分布表中的![]() ,
,![]() ;
;
(2)在扇形統(tǒng)計圖中,“排球”所在的扇形的圓心角為 度;
(3)全校有多少名學生選擇參加乒乓球運動?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知:如圖,在平面直角坐標系![]() 中,等邊
中,等邊![]() 的邊長為6,點
的邊長為6,點![]() 在邊
在邊![]() 上,點
上,點![]() 在邊
在邊![]() 上,且
上,且![]() .反比例函數(shù)
.反比例函數(shù)![]() 的圖象恰好經(jīng)過點
的圖象恰好經(jīng)過點![]() 和點
和點![]() .則
.則![]() 的值為 ( )
的值為 ( )
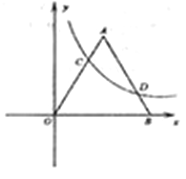
A.![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C為⊙O上一點,AD與過點C的切線互相垂直,垂足為點D,AD交⊙O于點E,連接CE,CB.
(1)求證:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的長.
,求AE的長.
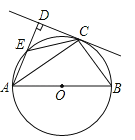
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com