
【題目】如圖,有一張長為8cm,寬為7cm的矩形紙片ABCD,現要剪下一個腰長為6cm的等腰三角形(要求:等腰三角形的一個頂點與矩形的一個頂點重合,其余的兩個頂點在矩形的邊上),則剪下的等腰三角形的面積為_____cm2.

【答案】18或3![]() 或12
或12![]()
【解析】分析:因為等腰三角形腰的位置不明確,所以分三種情況進行討論:
(1)△AEF為等腰直角三角形,直接利用面積公式求解即可;
(2)先利用勾股定理求出AE邊上的高BF,再代入面積公式求解;
(3)先求出AE邊上的高DF,再代入面積公式求解.
詳解:分三種情況計算:
(1)當AE=AF=6時,如圖:
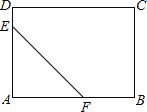
∴S△AEF=![]() AEAF=
AEAF=![]() ×6×6=18(cm2);
×6×6=18(cm2);
(2)當AE=EF=6時,如圖:
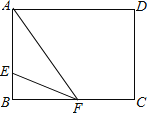
則BE=7-6=1,BF=![]() ,
,
∴S△AEF=![]() AEBF=
AEBF=![]() ×6×
×6×![]() =3
=3![]() (cm2);
(cm2);
(3)當AE=EF=6時,如圖:
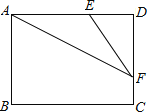
則DE=8-6=2,
DF=![]() ,
,
∴S△AEF=![]() AEDF=
AEDF=![]() ×6×4
×6×4![]() =12
=12![]() (cm2);
(cm2);
故答案為:18或3![]() 或12
或12![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,在正方形網格當中,三角形![]() 的三個頂點都在格點上.直線
的三個頂點都在格點上.直線![]() 與直線
與直線![]() 相交于點
相交于點![]() .
.
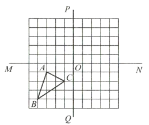
(1)畫出將三角形![]() 向右平移5個單位長度后的三角形
向右平移5個單位長度后的三角形![]() (點
(點![]() 的對應點分別是點
的對應點分別是點![]() ).
).
(2)畫出三角形![]() 關于直線
關于直線![]() 對稱的三角形
對稱的三角形![]() (點
(點![]() 的對應點分別是點
的對應點分別是點![]() ).
).
(3)畫出將三角形![]() 繞著點
繞著點![]() 旋轉
旋轉![]() 后的三角形
后的三角形![]() (點
(點![]() 的對應點分別是點
的對應點分別是點![]() ).
).
(4)在三角形![]() ,
,![]() ,
,![]() 中,三角形 與三角形 成軸對稱,三角形 與三角形 成中心對稱
中,三角形 與三角形 成軸對稱,三角形 與三角形 成中心對稱
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 與
與![]() 軸,
軸,![]() 軸分別交于點
軸分別交于點![]() ,B,與反比例函數圖象的一個交點為
,B,與反比例函數圖象的一個交點為![]() .
.
(1)求反比例函數的表達式;
(2)設直線![]() 與
與![]()
![]() 軸,
軸,![]() 軸分別交于點C,D,且
軸分別交于點C,D,且![]() ,直接寫出
,直接寫出![]() 的值 .
的值 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,對于任意點P,給出如下定義:若⊙P的半徑為1,則稱⊙P為點P的“伴隨圓”.
中,對于任意點P,給出如下定義:若⊙P的半徑為1,則稱⊙P為點P的“伴隨圓”.
(1)已知,點![]() ,
,
①點![]() 在點P的“伴隨圓” (填“上”或“內”或“外”);
在點P的“伴隨圓” (填“上”或“內”或“外”);
②點![]() 在點P的“伴隨圓” (填“上”或“內”或“外”);
在點P的“伴隨圓” (填“上”或“內”或“外”);
(2)若點P在![]() 軸上,且點P的“伴隨圓”與直線
軸上,且點P的“伴隨圓”與直線![]() 相切,求點P的坐標;
相切,求點P的坐標;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一元二次方程ax2+bx+c=0(a≠0)中,下列說法:
①若a+b+c=0,則b2﹣4ac>0;
②若方程兩根為﹣1和2,則2a+c=0;
③若方程ax2+c=0有兩個不相等的實根,則方程ax2+bx+c=0必有兩個不相等的實根;
④若b=2a+c,則方程有兩個不相等的實根.其中正確的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“龜兔首次賽跑”之后,輸了比賽的兔子沒有氣餒,總結反思后,和烏龜約定再賽一場.圖中的函數圖象刻畫了“龜兔再次賽跑”的故事(x表示烏龜從起點出發所行的時間,y1表示烏龜所行的路程,y2表示兔子所行的路程).有下列說法:

①“龜兔再次賽跑”的路程為1000米;
②兔子和烏龜同時從起點出發;
③烏龜在途中休息了10分鐘;
④兔子在途中750米處追上烏龜.
其中正確的說法是 .(把你認為正確說法的序號都填上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,點M、N是BC、CD邊上的點,連接AM、BN,若BM=CN

(1)求證:AM⊥BN
(2)將線段AM繞M順時針旋轉90°得到線段ME,連接NE,試說明:四邊形BMEN是平行四邊形;
(3)將△ABM繞A逆時針旋轉90°得到△ADF,連接EF,當![]()
![]() 時,請求出
時,請求出![]() 的值
的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校準備從甲乙兩位選手中選擇一位選手代表學校參加所在地區的漢字聽寫大賽,學校對兩位選手從表達能力、閱讀理解、綜合素質和漢字聽寫四個方面做了測試,他們各自的成績(百分制)如下表:
選手 | 表達能力 | 閱讀理解 | 綜合素質 | 漢字聽寫 |
甲 | 85 | 78 | 85 | 73 |
乙 | 73 | 80 | 82 | 83 |
(1)由表中成績已算得甲的平均成績為80.25,請計算乙的平均成績,從他們的這一成績看,應選派誰;
(2)如果表達能力、閱讀理解、綜合素質和漢字聽寫分別賦予它們20%、10%、30%和40%的權重,請分別計算兩名選手的最終成績,從他們的這一成績看,應選派誰.
查看答案和解析>>
科目:初中數學 來源: 題型:
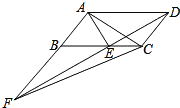
【題目】如圖,平行四邊形ABCD中,AE平分∠BAD,交BC于點E,且AB=AE,延長AB與DE的延長線交于點F.下列結論中:①△ABC≌△AED;②△ABE是等邊三角形;③AD=AF;④S△ABE=S△CDE;⑤S△ABE=S△CEF.其中正確的是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com