
【題目】已知:點M是平行四邊形ABCD對角線AC所在直線上的一個動點(點M不與點A、C重合),分別過點A、C向直線BM作垂線,垂足分別為點E、F,點O為AC的中點.
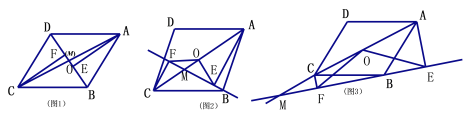
⑴如圖1,當點M與點O重合時,OE與OF的數量關系是 .
⑵直線BM繞點B逆時針方向旋轉,且∠OFE=30°.
①如圖2,當點M在線段AC上時,猜想線段CF、AE、OE之間有怎樣的數量關系?請你寫出來并加以證明;
②如圖3,當點M在線段AC的延長線上時,請直接寫出線段CF、AE、OE之間的數量關系.
【答案】(1)OE=OF;(2)①![]() ,詳見解析;②CF=OE-AE
,詳見解析;②CF=OE-AE
【解析】
(1)由△AOE≌△COF即可得出結論.
(2)①圖2中的結論為:CF=OE+AE,延長EO交CF于點N,只要證明△EOA≌△NOC,△OFN是等邊三角形,即可解決問題.
②圖3中的結論為:CF=OE-AE,延長EO交FC的延長線于點G,證明方法類似.
解:⑴∵ ![]()
∴AE∥CF
∴![]() 又
又![]() ,OA=OC
,OA=OC
∴△AOE≌△COF.
∴OE=OF.
⑵① ![]()
延長EO交CF延長線于N.

∵ ![]()
∴AE∥CF
∴![]() 又
又![]() ,OA=OC
,OA=OC
∴△OAE≌△OCN
∴AE=CN,OE=ON 又![]() ,
,![]()
∴OF=ON=OE, ![]()
∴OF=FN=ON=OE,又AE=CN
∴CF=AE-OE
②CF=OE-AE,證明如下:
延長EO交FC的延長線于點G

∵ ![]()
∴AE∥CF
∴∠G=∠AEO,∠OCG=∠EA0,
又∵AO=OC,
∴△OAE≌△OCG.
∴AE=CG,OG=OE.
又![]() ,
,![]()
∴OF=OG=OE, ![]()
∴△OGF是等邊三角形,
∴FG=OF=OE.
∴CF=OE-AE.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,對于點![]() 和
和![]() ,給出如下定義:
,給出如下定義:
如果 ,那么稱點
,那么稱點![]() 為點
為點![]() 的“伴隨點”.
的“伴隨點”.
例如:點![]() 的“伴隨點”為點
的“伴隨點”為點![]() ;點
;點![]() 的“伴隨點”為點
的“伴隨點”為點![]() .
.
(1)直接寫出點![]() 的“伴隨點”
的“伴隨點”![]() 的坐標.
的坐標.
(2)點![]() 在函數
在函數![]() 的圖象上,若其“伴隨點”
的圖象上,若其“伴隨點”![]() 的縱坐標為2,求函數
的縱坐標為2,求函數![]() 的解析式.
的解析式.
(3)點![]() 在函數
在函數![]() 的圖象上,且點
的圖象上,且點![]() 關于
關于![]() 軸對稱,點
軸對稱,點![]() 的“伴隨點”為
的“伴隨點”為![]() .若點
.若點![]() 在第一象限,且
在第一象限,且![]() ,求此時“伴隨點”
,求此時“伴隨點”![]() 的橫坐標.
的橫坐標.
(4)點![]() 在函數
在函數![]() 的圖象上,若其“伴隨點”
的圖象上,若其“伴隨點”![]() 的縱坐標
的縱坐標![]() 的最大值為
的最大值為![]() ,直接寫出實數
,直接寫出實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校為了解學生疫情期間一天在線學習時長,進行了一次隨機問卷調查(每人只能選擇其中一項),并將調查數據整理后繪成如下兩幅不完整的統計圖.請根據圖中信息解答下列問題:
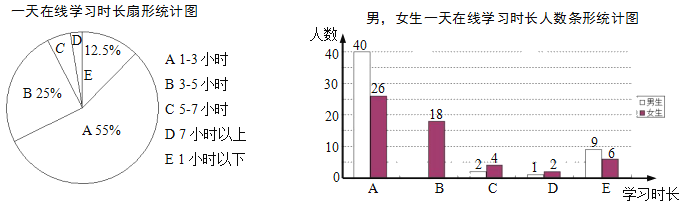
(1)求參與問卷調查的總人數.
(2)補全條形統計圖,并求出一天在線學習“5﹣7個小時”的扇形圓心角度數.
(3)若該校共有學生1800名,試估計全校一天在線學習“7小時以上”的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明是一名健步走運動的愛好者,他用手機軟件記錄了他近期健步走的步數(單位:萬步),繪制出如下的統計圖①和統計圖②,請根據相關信息,解答下列問題:
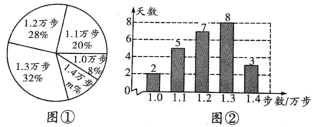
(Ⅰ)本次記錄的總天數為_____________,圖①中m的值為______________;
(Ⅱ)求小名近期健步走步數的平均數、眾數和中位數;
(Ⅲ)根據樣本數據,若小明堅持健步走一年(記為365天),試估計步數為1.1萬步的天數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點坐標分別為A(3,2)、B(3,5)、C(1,2).

⑴在平面直角坐標系中畫出△ABC關于原點對稱的△A1B1C1;
⑵把△ABC繞點A順時針旋轉一定的角度,得圖中的△AB2C2,點C2在AB上.請寫出:
①旋轉角為 度;
②點B2的坐標為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
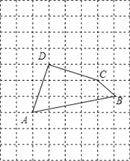
【題目】如圖,將四邊形ABCD放在每個小正方形的邊長為1的網格中,點A.B、C、D均落在格點上.
(Ⅰ)計算AD2+DC2+CB2的值等于_____;
(Ⅱ)請在如圖所示的網格中,用無刻度的直尺,畫出一個以AB為一邊的矩形,使該矩形的面積等于AD2+DC2+CB2,并簡要說明畫圖方法(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】矩形![]() 的兩條對稱軸為坐標軸,點
的兩條對稱軸為坐標軸,點![]() 的坐標為
的坐標為![]() .一張透明紙上畫有一個點
.一張透明紙上畫有一個點![]() 和一條拋物線,平移透明紙,使點
和一條拋物線,平移透明紙,使點![]() 與點
與點![]() 重合,此時拋物線的函數表達式為
重合,此時拋物線的函數表達式為![]() ,再次平移透明紙,使點
,再次平移透明紙,使點![]() 與點
與點![]() 重合,則該拋物線的函數表達式變為_______.
重合,則該拋物線的函數表達式變為_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,![]() 是等邊三角形,點
是等邊三角形,點![]() ,點
,點![]() ,點
,點![]() 是
是![]() 邊上的一個動點(與點
邊上的一個動點(與點![]() 、
、![]() 不重合).直線
不重合).直線![]() 是經過點
是經過點![]() 的一條直線,把
的一條直線,把![]() 沿直線
沿直線![]() 折疊,點
折疊,點![]() 的對應點是點
的對應點是點![]() .
.
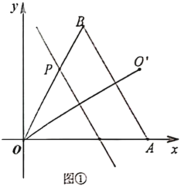
(1)如圖①,當![]() 時,若直線
時,若直線![]() ,求點
,求點![]() 的坐標;
的坐標;
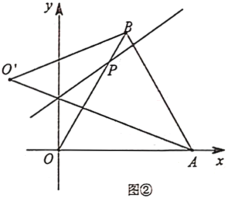
(2)如圖②,當點![]() 在
在![]() 邊上運動時,若直線
邊上運動時,若直線![]() ,求
,求![]() 的面積;
的面積;
(3)當![]() 時,在直線
時,在直線![]() 變化過程中,求
變化過程中,求![]() 面積的最大值(直接寫出結果即可).
面積的最大值(直接寫出結果即可).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com