【題目】四邊形ABCD是菱形，對角線AC=8cm，BD=6cm，DH⊥AB于H，求DH的長．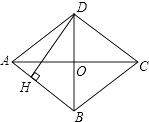 
【答案】解：∵四邊形ABCD是菱形，AC=8cm，BD=6cm， ∴AC⊥BD，OA= 
AC=4cm，OB= BD=3cm，
∴Rt△AOB中，AB= 
= 
=5，
∵DH⊥AB，
∵菱形ABCD的面積S= ACBD=ABDH， ×6×8=5DH，
∴DH= 
【解析】先根據菱形對角線互相垂直平分得：OA= 
AC=4cm，OB= BD=3cm，根據勾股定理求得AB=5cm，由菱形面積公式的兩種求法列式可以求得高DH的長．
【考點精析】利用菱形的性質對題目進行判斷即可得到答案，需要熟知菱形的四條邊都相等；菱形的對角線互相垂直，并且每一條對角線平分一組對角；菱形被兩條對角線分成四個全等的直角三角形；菱形的面積等于兩條對角線長的積的一半．
導學與測試系列答案
新非凡教輔沖刺100分系列答案科目：初中數學 來源： 題型：
【題目】小明用的練習本可以到甲商店購買，也可以到乙商店購買，已知兩商店的標價都是每本1元，甲商店的優惠條件是：購買10本以上，從第11本開始按標價的70%賣；乙商店的優惠條件是：每本按標價的80%賣．
(1)小明要買20本時，到哪個商店較省錢？
(2)買多少本時到兩個商店付的錢一樣？
(3)小明現有32元錢，最多可買多少本？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】我國漢代數學家趙爽為了證明勾股定理，創制了一幅“弦圖”，后人稱其為“趙爽弦圖”（如圖（1））．圖（2）由弦圖變化得到，它是由八個全等的直角三角形拼接而成，記圖中正方形ABCD、正方形EFGH、正方形MNKT的面積分別為S1、S2、S3 ． 若正方形EFGH的邊長為2，則S1+S2+S3= ．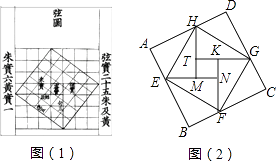 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在數軸上點A表示的數為a，點B表示的數為b，且a，b滿足|a+2|+（3a+b）2=0，O為原點．
（1）則a= ，b= ；
（2）若動點P從點A出發，以每秒1個單位長度的速度沿數軸向右勻速運動，
①當PO=2PB時，求點P的運動時間t；
②當點P運動到線段OB上時，分別取AP和OB的中點E、F，則
的值是否為一個定值？如果是，求出定值，如果不是，說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
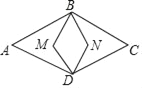
【題目】如圖，菱形ABCD內兩點M、N，滿足MB⊥BC，MD⊥DC，NB⊥BA，ND⊥DA，若四邊形BMDN的面積是菱形ABCD面積的
，則cosA= ______ ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】2015年1月，市教育局在全市中小學中選取了63所學校從學生的思想品德、學業水平、學業負擔、身心發展和興趣特長五個維度進行了綜合評價．評價小組在選取的某中學七年級全體學生中隨機抽取了若干名學生進行問卷調查，了解他們每天在課外用于學習的時間，并繪制成如下不完整的統計圖． 根據上述信息，解答下列問題：
（1）本次抽取的學生人數是 ______ ；扇形統計圖中的圓心角α等于 ______ ；補全統計直方圖；
（2）被抽取的學生還要進行一次50米跑測試，每5人一組進行．在隨機分組時，小紅、小花兩名女生被分到同一個小組，請用列表法或畫樹狀圖求出她倆在抽道次時抽在相鄰兩道的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
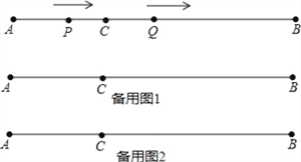
【題目】如圖，AB=12cm，點C是線段AB上的一點，BC=2AC．動點P從點A出發，以3cm/s的速度向右運動，到達點B后立即返回，以3cm/s的速度向左運動；動點Q從點C出發，以1cm/s的速度向右運動．設它們同時出發，運動時間為ts．當點P與點Q第二次重合時，P、Q兩點停止運動．
（1）AC=__cm，BC=__cm；
（2）當t為何值時，AP=PQ；
（3）當t為何值時，PQ=1cm．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
