
【題目】我國漢代數學家趙爽為了證明勾股定理,創制了一幅“弦圖”,后人稱其為“趙爽弦圖”(如圖(1)).圖(2)由弦圖變化得到,它是由八個全等的直角三角形拼接而成,記圖中正方形ABCD、正方形EFGH、正方形MNKT的面積分別為S1、S2、S3 . 若正方形EFGH的邊長為2,則S1+S2+S3= . 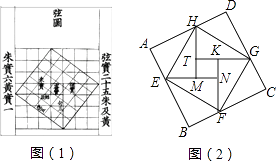
【答案】12
【解析】解:∵八個直角三角形全等,四邊形ABCD,EFGH,MNKT是正方形, ∴CG=KG,CF=DG=KF,
∴S1=(CG+DG)2
=CG2+DG2+2CGDG
=GF2+2CGDG,
S2=GF2 ,
S3=(KF﹣NF)2=KF2+NF2﹣2KFNF,
∴S1+S2+S3=GF2+2CGDG+GF2+KF2+NF2﹣2KFNF=3GF2=12,
故答案是:12.
根據八個直角三角形全等,四邊形ABCD,EFGH,MNKT是正方形,得出CG=KG,CF=DG=KF,再根據S1=(CG+DG)2 , S2=GF2 , S3=(KF﹣NF)2 , S1+S2+S3=12得出3GF2=12.


科目:初中數學 來源: 題型:
【題目】已知函數 ![]() 的圖象經過點(2,3),下列說法正確的是( )
的圖象經過點(2,3),下列說法正確的是( )
A.y隨x的增大而增大
B.函數的圖象只在第一象限
C.當x<0時,必有y<0
D.點(﹣2,﹣3)不在此函數圖象上
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數y1=![]() 與一次函數y2=k2x+b的圖象交于點A(1,8),B(-4,m)兩點.
與一次函數y2=k2x+b的圖象交于點A(1,8),B(-4,m)兩點.
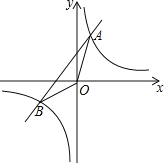
(1)求k1,k2,b的值;
(2)求△AOB的面積;
(3)請直接寫出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數y1=![]() 與一次函數y2=k2x+b的圖象交于點A(1,8),B(-4,m)兩點.
與一次函數y2=k2x+b的圖象交于點A(1,8),B(-4,m)兩點.
(1)求k1,k2,b的值;
(2)求△AOB的面積;
(3)請直接寫出不等式![]() x+b的解.
x+b的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,M是邊AB的中點,D是邊BC延長線上的一點,且CD= ![]() BC,作DN∥CM交AC于點N.求證:四邊形MCDN是平行四邊形.
BC,作DN∥CM交AC于點N.求證:四邊形MCDN是平行四邊形. 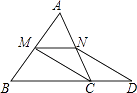
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com