
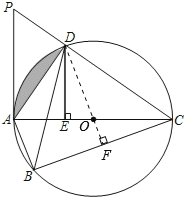
【題目】如圖所示,四邊形![]() 內接于⊙
內接于⊙![]() ,
,![]() 是⊙
是⊙![]() 的直徑,過點
的直徑,過點![]() 的切線與
的切線與![]() 的延長線相交于點
的延長線相交于點![]() .且
.且![]() ,連接
,連接![]() .
.

(1)求證:![]() ;
;
(2)過點![]() 作
作![]() ,垂足為
,垂足為![]() ,當
,當![]() 時,求⊙
時,求⊙![]() 的半徑;
的半徑;
(3)在(2)的條件下,求陰影部分的面積.
【答案】(1)見解析;(2)半徑![]() ;(3)
;(3)![]()
![]()
【解析】
(1)作DF⊥BC于F,根據切線的性質得到∠PAC=90°,根據圓周角定理得到∠ADC=90°,得到∠DBC=∠DCB,得到DB=DC;
(2)根據垂徑定理求出FC,證明△DEC≌△CFD,根據全等三角形的性質得到DE=FC=![]() ,根據tan∠DAE=
,根據tan∠DAE=![]() =
=![]() ,求得∠DAE=60°,從而可證得△AOD是等邊三角形,則⊙O的半徑OD=AD=2.
,求得∠DAE=60°,從而可證得△AOD是等邊三角形,則⊙O的半徑OD=AD=2.
(3)根據△AOD是等邊三角形得∠AOD=60°,再根據陰影部分的面積=扇形AOD的面積﹣△AOD的面積計算即可.
(1)證明:![]() 是⊙
是⊙![]() 的切線,
的切線,
![]() ,即
,即![]() ,
,
![]() 是⊙
是⊙![]() 的直徑,
的直徑,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
;
(2)解:如圖,作![]() 于
于![]() ,連接
,連接![]()
![]()
![]() 是
是![]() 的垂直平分線,
的垂直平分線,
![]() 經過點
經過點![]()
![]()
![]()
在![]() 和
和![]() 中,
中,
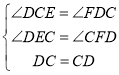
![]()
![]()
![]()
![]()
![]()
在△AED中,DE=![]() ,AE=1,
,AE=1,
則tan∠DAE=![]() =
=![]() ,
,
∴∠DAE=60°.
又∵OD=OA,
∴△AOD是等邊三角形,
∴⊙O的半徑OD=AD=2.
(3)解:∵△AOD是等邊三角形,
∴∠AOD=60°.
∴![]()
![]()


 輕巧奪冠周測月考直通中考系列答案
輕巧奪冠周測月考直通中考系列答案科目:初中數學 來源: 題型:
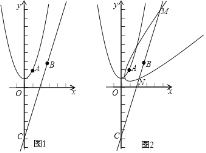
【題目】如圖1,已知拋物線的頂點坐標為(0,1)且經過點A(1,2),直線y=3x﹣4![]() 經過點B(
經過點B(![]() ,n),與y軸交點為C.
,n),與y軸交點為C.
(1)求拋物線的解析式及n的值;
(2)將直線BC繞原點O逆時針旋轉45°,求旋轉后的直線的解析式;
(3)如圖2將拋物線繞原點O順時針旋轉45°得到新曲線,新曲線與直線BC交于點M、N,點M在點N的上方,求點N的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形![]() 中,對角線
中,對角線![]() 相交于點
相交于點![]() ,以
,以![]() 為邊向外作等邊
為邊向外作等邊![]() ,連接
,連接![]() 交
交![]() 于
于![]() 若點
若點![]() 為
為![]() 的延長線上一點,連接
的延長線上一點,連接![]() ,連接
,連接![]() 且
且![]() 平分
平分![]() ,下列選項正確的有( )
,下列選項正確的有( )
①![]() ;②
;②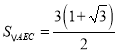 ;③
;③![]() ;④
;④![]()

A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知等腰直角![]() 中,
中,![]() ,點
,點![]() 是
是![]() 邊上一點,以
邊上一點,以![]() 為邊作等腰直角
為邊作等腰直角![]() ,其中
,其中![]() ,邊
,邊![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() 是
是![]() 上一點.
上一點.
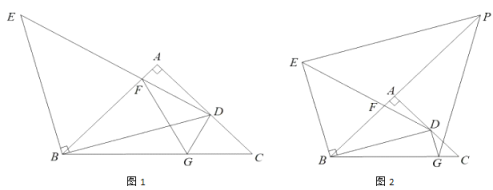
(1)如圖1,若![]() ,連接
,連接![]() .
.
①若![]() ,求
,求![]() 的長度;
的長度;
②求證:![]() ;
;
(2)如圖2,若![]() 交
交![]() 的延長線于點
的延長線于點![]() ,連接
,連接![]() ,請猜想線段
,請猜想線段![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,點C是![]() 的中點,連接AC并延長至點D,使CD=AC,點E是OB上一點,且
的中點,連接AC并延長至點D,使CD=AC,點E是OB上一點,且![]() ,CE的延長線交DB的延長線于點F,AF交⊙O于點H,連接BH.
,CE的延長線交DB的延長線于點F,AF交⊙O于點H,連接BH.

(1)求證:BD是⊙O的切線;(2)當OB=2時,求BH的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
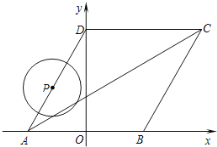
【題目】如圖所示,菱形ABCD的頂點A、B在![]() 軸上,點A在點B的左側,點D在
軸上,點A在點B的左側,點D在![]() 軸的正半軸上,
軸的正半軸上,![]() ,點A的坐標為
,點A的坐標為![]() .
.
(1)求D點的坐標.
(2)求直線AC的函數關系式.
(3)動點P從點A出發,以每秒1個單位長度的速度,按照![]() 的順序在菱形的邊上勻速運動一周,設運動時間為
的順序在菱形的邊上勻速運動一周,設運動時間為![]() 秒.求
秒.求![]() 為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
為何值時,以點P為圓心、以1為半徑的圓與對角線AC相切?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,D是![]() 的中點,E為OD延長線上一點,且∠CAE=2∠C,AC與BD交于點H,與OE交于點F.
的中點,E為OD延長線上一點,且∠CAE=2∠C,AC與BD交于點H,與OE交于點F.
(1)求證:AE是⊙O的切線;
(2)若DH=9,tanC=![]() ,求直徑AB的長.
,求直徑AB的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com