
【題目】圖1所示是一枚質地均勻的骰子.骰子有六個面并分別代表數字1,2,3,4,5,6.如圖2,正六邊形ABCDEF的頂點處各有一個圈.跳圈游戲的規則為:游戲者每擲一次骰子,骰子向上的一面上的點數是幾,就沿正六邊形的邊順時針方向連續跳幾個邊長.如:若從圈A起跳,第一次擲得3,就順時針連續跳3個邊長,落到圈D;若第二次擲得2,就從圈D開始順時針連續跳2個邊長,落到圈F……
設游戲者從圈A起跳.
(1)小明隨機擲一次骰子,求落回到圈A的概率P1;
(2)小亮隨機擲兩次骰子,用列表法或畫樹狀圖法求最后落回到圈A的概率P2,并指出他與小明落回到圈A的可能性一樣嗎?
 圖1
圖1 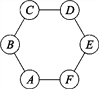 圖2
圖2
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,三角形A`B`C`是由三角形ABC經過某種平移得到的,點A與點A`,點B與點B`,點C與點C`分別對應,觀察點與點坐標之間的關系,解答下列問題:

![]() 分別寫出點A、點B、點C、點A`、點B`、點C`的坐標,并說明三角形A`B`C`是由三角形ABC經過怎樣的平移得到的.
分別寫出點A、點B、點C、點A`、點B`、點C`的坐標,并說明三角形A`B`C`是由三角形ABC經過怎樣的平移得到的.
![]() 若點
若點![]() 是點
是點![]() 通過
通過![]() 中的平移變換得到的,求
中的平移變換得到的,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
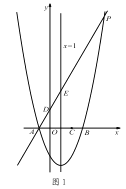
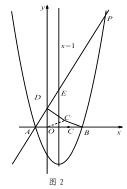
【題目】如圖1,對稱軸為直線x=1的拋物線y=![]() x2+bx+c,與x軸交于A、B兩點(點A在點B的左側),且點A坐標為(-1,0).又P是拋物線上位于第一象限的點,直線AP與y軸交于點D,與拋物線對稱軸交于點E,點C與坐標原點O關于該對稱軸成軸對稱.
x2+bx+c,與x軸交于A、B兩點(點A在點B的左側),且點A坐標為(-1,0).又P是拋物線上位于第一象限的點,直線AP與y軸交于點D,與拋物線對稱軸交于點E,點C與坐標原點O關于該對稱軸成軸對稱.
(1)求點 B 的坐標和拋物線的表達式;
(2)當 AE:EP=1:4 時,求點 E 的坐標;
(3)如圖 2,在(2)的條件下,將線段 OC 繞點 O 逆時針旋轉得到 OC ′,旋轉角為 α(0°<α<90°),連接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數軸上點A表示-3,點B表示4.
(1)點A與點B之間的距離是 ;
(2)我們知道,在數軸上|a|表示數a所對應的點到原點的距離,你能說明![]() 在數軸上表示的意義嗎?
在數軸上表示的意義嗎?
(3)在數軸上點P表示的數為x,是否存在這樣的點P,使2PA+PB=12?若存在,請求出相應的x;若不存在,請說明理由.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】自我國實施“限塑令”起,開始有償使用環保購物袋,為了滿足市場需求,某廠家生產A、B兩種款式的布質環保購物袋,每天生產4500個,兩種購物袋的成本和售價如下表,若設每天生產A種購物袋 x個.
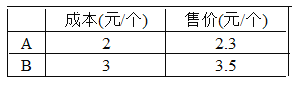
(1)用含x的整式表示每天的生產成本,并進行化簡;
(2)用含x的整式表示每天獲得的利潤,并進行化簡(利潤=售價-成本);
(3)當x=1500時,求每天的生產成本與每天獲得的利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學活動
問題情境:
如圖1,在ABC中,AB=AC,∠BAC=90°,D,E分別是邊AB,AC的中點,將ADE繞點A順時針旋轉α角(0°<α<90°)得到AD′E′,連接CE′,BD′.探究CE′與BD′的數量關系;
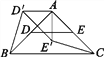 圖1
圖1 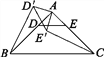 圖2
圖2 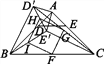 圖3
圖3 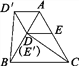 圖4
圖4
探究發現:
(1)圖1中,CE′與BD′的數量關系是________;
(2)如圖2,若將問題中的條件“D,E分別是邊AB,AC的中點”改為“D為AB邊上任意一點,DE∥BC交AC于點E”,其他條件不變,(1)中CE′與BD′的數量關系還成立嗎?請說明理由;
拓展延伸:
(3)如圖3,在(2)的條件下,連接BE′,CD′,分別取BC,CD′,E′D′,BE′的中點F,G,H,I,順次連接F,G,H,I得到四邊形FGHI.請判斷四邊形FGHI的形狀,并說明理由;
(4)如圖4,在ABC中,AB=AC,∠BAC=60°,點D,E分別在AB,AC上,且DE∥BC,將ADE繞點A順時針旋轉60°得到AD′E′,連接CE′,BD′.請你仔細觀察,提出一個你最關心的數學問題(例如:CE′與BD′相等嗎?).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,在△ABC中,∠ACB=90°,AC=BC,直線l過點C,點A,B在直線l同側,BD⊥l,AE⊥l,垂足分別為D,E.求證:△AEC≌△CDB.
(2)如圖2,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,利用(1)中的結論,請按照圖中所標注的數據計算圖中實線所圍成的圖形的面積S= .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,AB=12,點E在邊CD上,且BG=CG,將△ADE沿AE對折至△AFE,延長EF交邊BC于點G,連接AG、CF.下列結論:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正確結論的個數是( )
.其中正確結論的個數是( )

A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com