
【題目】如圖,Rt△ABC中,∠ACB=90°.

(1)以點C為圓心,以CB的長為半徑畫弧,交AB于點G,分別以點G,B為圓心,以大于![]() GB的長為半徑畫弧,兩弧交于點K,作射線CK;
GB的長為半徑畫弧,兩弧交于點K,作射線CK;
(2)以點B為圓心,以適當的長為半徑畫弧,交BC于點M,交AB的延長線于點N,分別以點M,N為圓心,以大于![]() MN的長為半徑畫弧,兩弧交于點P,作直線BP交AC的延長線于點D,交射線CK于點E;
MN的長為半徑畫弧,兩弧交于點P,作直線BP交AC的延長線于點D,交射線CK于點E;
(3)過點D作DF⊥AB交AB的延長線于點F,連接CF.
根據以上操作過程及所作圖形,有如下結論:
①CE=CD;
②BC=BE=BF;
③![]() ;
;
④∠BCF=∠BCE.
所有正確結論的序號為( )
A.①②③B.①③C.②④D.③④
【答案】B
【解析】
①由作圖過程可得,CE是BG的垂直平分線,BD是∠CBF的平分線,可以證明△BCD≌△BFD,根據全等三角形的性質進而可以判斷;
②根據BC≠BE,即可判斷;
③根據S四邊形CDFB=S△BCD+S△BFD即可判斷;
④根據△BCE與△BCF不全等,∠BCE≠∠BCF,即可判斷.
如圖,連接CF,交BD于點H,
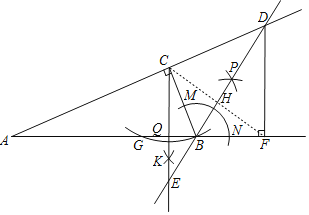
由作圖過程可知:
CE是BG的垂直平分線,BD是∠CBF的平分線,
設CE與AB交于點Q,
∴∠CQA=∠DFA=90°,
∴CQ∥DF,
∴∠CED=∠FDE,
∵BD是∠CBF的平分線,
∴∠CBD=∠FBD,
∵∠BCD=∠BFD=90°,
BD=BD,
∴△BCD≌△BFD(AAS),
∴∠CDB=∠FDB,
∴∠CDB=∠CED,
∴CE=CD,
所以①正確;
∵△BCD≌△BFD(AAS),
∴BC=BF,
但是BC≠BE,
∴②不正確;
∵S四邊形CDFB=S△BCD+S△BFD
=![]() BDCH+
BDCH+![]() BDFH
BDFH
=![]() CFBD.
CFBD.
∴③正確;
∵△BCE與△BCF不全等,
∴∠BCE≠∠BCF,
∴④不正確.
所以正確結論的序號為①③.
故選:B.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
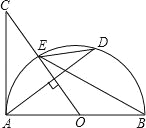
【題目】如圖,AB是半圓O的直徑,過點O作弦AD的垂線交半圓O于點E,交AC于點C,使∠BED=∠C.
(1)判斷直線AC與圓O的位置關系,并證明你的結論;
(2)若AC=8,cos∠BED=![]() ,求AD的長.
,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形![]() 中,
中,![]() .點
.點![]() 從點
從點![]() 出發,沿
出發,沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() 同時,點
同時,點![]() 從點
從點![]() 出發,沿
出發,沿![]() 方向勻速運動,速度為
方向勻速運動,速度為![]() .過點
.過點![]() 作
作![]() 交
交![]() 于點
于點![]() ,連
,連![]() 接,交
接,交![]() 于點
于點![]() .設運動時間為
.設運動時間為![]() .解答下列問題:
.解答下列問題:
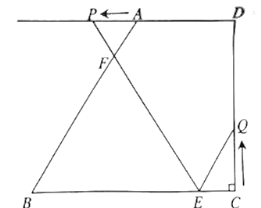
(1)當![]() 為何值時,
為何值時,![]() ?
?
(2)設五邊形![]() 的面積為
的面積為![]() , 求
, 求![]() 與
與![]() 的函數關系式;
的函數關系式;
(3)連接![]() .是否存在某一時刻
.是否存在某一時刻![]() , 使點
, 使點![]() 在
在![]() 的垂直平分線上,若存在,求出的值;若不存在,說明理由.
的垂直平分線上,若存在,求出的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場舉辦抽獎活動,規則如下:在不透明的袋子中有2個紅球和2個黑球,這些球除顏色外都相同,顧客每次摸出一個球,若摸到紅球,則獲得1份獎品,若摸到黑球,則沒有獎品。
(1)如果小芳只有一次摸球機會,那么小芳獲得獎品的概率為 ;
(2)如果小芳有兩次摸球機會(摸出后不放回),求小芳獲得2份獎品的概率。(請用“畫樹狀圖”或“列表”等方法寫出分析過程)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于二次函數y=x2+2x+3的圖象有以下說法:其中正確的個數是( )
①它開口向下;②它的對稱軸是過點(﹣1,3)且平行于y軸的直線;③它與x軸沒有公共點;④它與y軸的交點坐標為(3,0).
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學數學興趣小組在一次課外學習與探究中遇到一些新的數學符號,他們將其中某些材料摘錄如下:
對于三個實,數![]() ,
,![]() ,
,![]() ,用
,用![]() 表示這三個數的平均數,用
表示這三個數的平均數,用![]() 表示這三個數中最小的數,例如
表示這三個數中最小的數,例如![]()
![]() =4,
=4,![]() ,
,![]() .請結合上述材料,解決下列問題:
.請結合上述材料,解決下列問題:
(1)①![]() _____,
_____,
②![]() _____;
_____;
(2)若![]() ,則
,則![]() 的取值范圍為_____;
的取值范圍為_____;
(3)若![]() ,求
,求![]() 的值;
的值;
(4)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
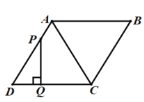
【題目】如圖,四邊形![]() 是菱形,
是菱形,![]() ,點
,點![]() 從
從![]() 點出發,沿
點出發,沿![]() 運動,過點
運動,過點![]() 作直線
作直線![]() 的垂線,垂足為
的垂線,垂足為![]() ,設點
,設點![]() 運動的路程為
運動的路程為![]() ,
,![]() 的面積為
的面積為![]() ,則下列圖象能正確反映
,則下列圖象能正確反映![]() 與
與![]() 之間的函數關系的是( ).
之間的函數關系的是( ).
A.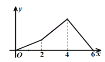 B.
B.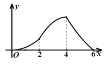 C.
C.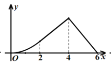 D.
D.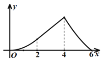
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若二次函數![]() 圖象的頂點在一次函數
圖象的頂點在一次函數![]() 的圖象上,則稱
的圖象上,則稱![]() 為
為![]() 的中雅函數,如:
的中雅函數,如:![]() 是
是![]() 的中雅函數.
的中雅函數.
(1)判斷二次函數![]() 是否為一次函數
是否為一次函數![]() 的中雅函數,并說明理由;
的中雅函數,并說明理由;
(2)若關于![]() 的一次函數
的一次函數![]() 的中雅函數
的中雅函數![]() 與
與![]() 軸兩個交點間的距離為
軸兩個交點間的距離為![]() ,求直線
,求直線![]() 與坐標軸所圍三角形的面積;
與坐標軸所圍三角形的面積;
(3)已知關于![]() 的一次函數
的一次函數![]() 的中雅函數為
的中雅函數為![]() ,與
,與![]() 平行的直線
平行的直線![]() 交中雅函數
交中雅函數![]() 的圖象于
的圖象于![]() 、
、![]() 兩點,若
兩點,若![]() 軸上有且僅有一個點
軸上有且僅有一個點![]() ,使得
,使得![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某賓館有若干間標準房,當標準房的價格為![]() 元時,每天入住的國間數為
元時,每天入住的國間數為![]() 間,經市場調查表明,該賓館每間標準房的價格在
間,經市場調查表明,該賓館每間標準房的價格在![]() 元之間(含
元之間(含![]() 元,
元,![]() 元)浮動時,每天人住的房間數
元)浮動時,每天人住的房間數![]() (間)與每間標準房的價格
(間)與每間標準房的價格![]() (元)的數據如下表:
(元)的數據如下表:
| …… | 190 | 200 | 210 | 220 | …… |
| …… | 65 | 60 | 55 | 50 | …… |
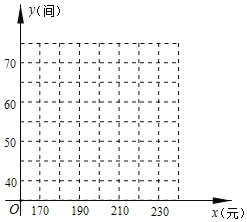
(1)根據所給數據在坐標系中描出相應的點,并畫出圖象.
(2)猜想(1)中的圖象是什么函數的圖象,求![]() 關于
關于![]() 的函數表達式,并寫出自變量
的函數表達式,并寫出自變量![]() 的取值范圍.
的取值范圍.
(3)設客房的日營業額為W (元).若不考慮其他因素,問賓館標準房的價格定為多少元時,客房的日營業額最大?最大為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com