
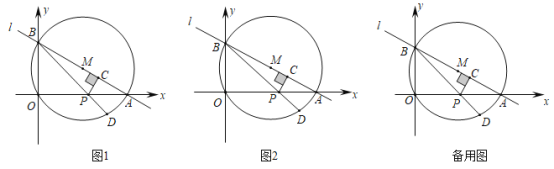
【題目】如圖1,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,以
,以![]() 為直徑作
為直徑作![]() ,點
,點![]() 為線段
為線段![]() 上一動點(與點O、A不重合),作
上一動點(與點O、A不重合),作![]() 于
于![]() ,連結
,連結![]() 并延長交
并延長交![]() 于點
于點![]() .
.
(1)求點![]() 的坐標和
的坐標和![]() 的值;
的值;
(2)設![]() .
.
①當![]() 時,求
時,求![]() 的值及點
的值及點![]() 的坐標;
的坐標;
②求![]() 關于
關于![]() 的函數表達式.
的函數表達式.
(3)如圖2,連接![]() ,當點
,當點![]() 在線段
在線段![]() 上運動時,求
上運動時,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;
;![]() =
=![]() ;(2)①
;(2)①![]() ,點
,點![]() 的坐標為
的坐標為![]() ;②
;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)令x=0求出y值可得B點坐標,令y=0求出x值可得A點坐標;根據A、B坐標可知OA、OB的長,根據正切的定義即可得![]() 的值;
的值;
(2)①由x=1可得點C與點M重合,如圖1,連接![]() ,作
,作![]() 于
于![]() ,設
,設![]() ,則
,則![]() ,由垂徑定理可得PA=PB,利用勾股定理可求出a值,根據正切的定義即可得出y值,可得PA的長,由AB是直徑可知
,由垂徑定理可得PA=PB,利用勾股定理可求出a值,根據正切的定義即可得出y值,可得PA的長,由AB是直徑可知![]() ,可得
,可得![]() ,即可求出AD、PD的長,利用面積法及勾股定理即可求出DH、PH的長,進而可得點D坐標;
,即可求出AD、PD的長,利用面積法及勾股定理即可求出DH、PH的長,進而可得點D坐標;
②如圖2,作![]() 交
交![]() 軸于點
軸于點![]() ,可得
,可得![]() ,可求出OE=2,根據平行線分線段成比例定理可得
,可求出OE=2,根據平行線分線段成比例定理可得![]() ,可用x表示出OP的長,根據正切的定義即可得出y與x的關系式;
,可用x表示出OP的長,根據正切的定義即可得出y與x的關系式;
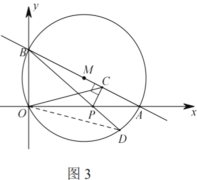
(3)如圖3,連接![]() ,由
,由![]() 可證明
可證明![]() ,根據相似三角形的性質可得
,根據相似三角形的性質可得![]() ,即可證明
,即可證明![]() ,可得
,可得![]() ,進而可證明
,進而可證明![]() ,根據相似三角形的性質可得
,根據相似三角形的性質可得![]() ,設
,設![]() ,則
,則![]() ,即可用t表示出
,即可用t表示出![]() ,根據二次函數的性質即可求出
,根據二次函數的性質即可求出![]() 的最大值.
的最大值.
(1)∵![]() ,
,
∴當![]() 時,
時,![]() ,當
,當![]() 時,
時,![]() ,
,
∴![]() ,
,
∴OA=8,OB=4,
∵![]() ,
,
∴![]() .
.
(2)①當![]() 時,
時,![]() ,
,
∴![]() ,即點
,即點![]() 與
與![]() 重合,
重合,
如圖1,連接![]() ,作
,作![]() 于
于![]() ,設
,設![]() ,則
,則![]() ,
,
![]()
![]()
在![]() 中,
中,![]() ,
,
解得![]() ,
,
![]() ,
,
![]() 是
是![]() 的直徑,
的直徑,
∴![]()
∴![]() ,
,
設PD=x,則AD=![]() x,
x,
∴x2+(![]() x)2=52,
x)2=52,
解得:x=3,(負值舍去)即PD=3,
∴AD=![]() x=4,
x=4,
![]() ,
,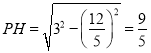 ,
,
![]() ,
,
∵點D在第四象限,
∴點![]() 的坐標為
的坐標為![]()
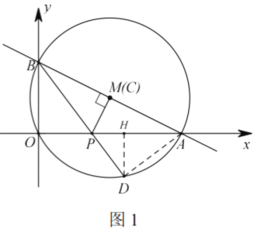
②如圖2,作![]() 交
交![]() 軸于點
軸于點![]() ;
;
![]()
![]() ,
,
![]()
![]()
![]()
![]()
即![]()
![]()
![]()
![]() 關于
關于![]() 的函數表達式為
的函數表達式為![]()
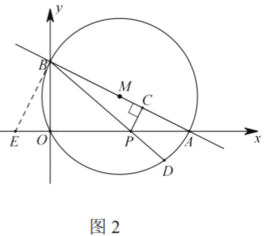
(3)如圖3,連接![]() ,
,
∵OA=8,OB=4,
∴AB=![]() ,
,
∵![]()
![]()
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
設![]() ,則
,則![]() ,
,
∴![]()
![]() ,
,
![]() 當
當![]() 時,
時,![]() 的最大值為
的最大值為![]() .
.


科目:初中數學 來源: 題型:
【題目】已知:△ABC為等邊三角形.
(1)求作:△ABC的外接圓⊙O.(不寫作法,保留作圖痕跡)
(2)射線AO交BC于點D,交⊙O于點E,過E作⊙O的切線EF,與AB的延長線交于點F.
①根據題意,將(1)中圖形補全;
②求證:EF∥BC;
③若DE=2,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
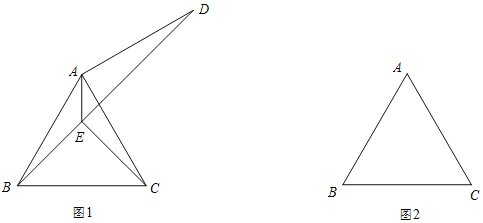
【題目】已知,如圖,△ABC是等邊三角形.
(1)如圖1,將線段AC繞點A逆時針旋轉90°,得到AD,連接BD,∠BAC的平分線交BD于點E,連接CE.
①求∠AED的度數;
②用等式表示線段AE、CE、BD之間的數量關系(直接寫出結果).
(2)如圖2,將線段AC繞點A順時針旋轉90°,得到AD,連接BD,∠BAC的平分線交DB的延長線于點E,連接CE.
①依題意補全圖2;
②用等式表示線段AE、CE、BD之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,拋物線y![]() x2bxc與直線y
x2bxc與直線y![]() x3分別交于x軸,y軸上的B,C兩點,設該拋物線與x軸的另一個交點為A,頂點為D,連接CD交x軸于點E.
x3分別交于x軸,y軸上的B,C兩點,設該拋物線與x軸的另一個交點為A,頂點為D,連接CD交x軸于點E.
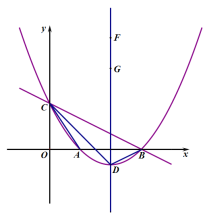
(1)求該拋物線的函數表達式;
(2)求該拋物線的對稱軸和D點坐標;
(3)點F,G是對稱軸上兩個動點,且FG=2,點F在點G的上方,請直接寫出四邊形ACFG的周長的最小值;
(4)連接BD,若P在y軸上,且∠PBC=∠DBA+∠DCB,請直接寫出點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了解學生對“防溺水”安全知識的掌握情況,從全校![]() 名學生中隨機抽取部分學生進行測試,并將測試成績(百分制,得分均為整數)進行統計分析,繪制了如下不完整的頻數表和頻數直方圖.
名學生中隨機抽取部分學生進行測試,并將測試成績(百分制,得分均為整數)進行統計分析,繪制了如下不完整的頻數表和頻數直方圖.
被抽取的部分學生安全知識測試成績頻數表
組別 | 成績(分) | 頻數(人) | 頻率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
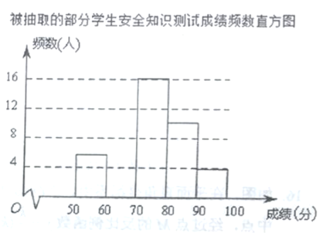
由圖表中給出的信息回答下列問題:
![]() 表中的
表中的![]() ;抽取部分學生的成績的中位數在 組;
;抽取部分學生的成績的中位數在 組;
![]() 把上面的頻數直方圖補充完整;
把上面的頻數直方圖補充完整;
![]() 如果成績達到
如果成績達到![]() 分以上(包括
分以上(包括![]() 分)為優秀,請估計該校
分)為優秀,請估計該校![]() 名學生中成績優秀的人數.
名學生中成績優秀的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
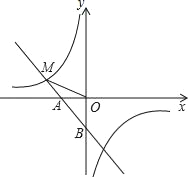
【題目】如圖,一次函數y1=﹣x﹣1的圖象與x軸交于點A,與y軸交于點B,與反比例函數![]() 圖象的一個交點為M(﹣2,m).
圖象的一個交點為M(﹣2,m).
(1)求反比例函數的解析式;
(2)當y2>y1時,求x的取值范圍;
(3)求點B到直線OM的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平行四邊形ABCD中,對角線AC,BD交于點O,E是邊AD上的一個動點(與點A,D不重合),連接EO并延長,交BC于點F,連接BE,DF.下列說法:
① 對于任意的點E,四邊形BEDF都是平行四邊形;
② 當∠ABC>90°時,至少存在一個點E,使得四邊形BEDF是矩形;
③ 當AB<AD時,至少存在一個點E,使得是四邊形BEDF是菱形;
④ 當∠ADB=45°時,至少存在一個點E,使得是四邊形BEDF是正方形.
所有正確說法的序號是:_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,二次函數y=x2﹣2mx+1圖象與y軸的交點為A,將點A向右平移4個單位長度得到點B.
(1)直接寫出點A與點B的坐標;
(2)求出拋物線的對稱軸(用含m的式子表示);
(3)若函數y=x2﹣2mx+1的圖象與線段AB恰有一個公共點,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】體育老師為了解本校九年級女生1分鐘“仰臥起坐”體育測試項目的達標情況,從該校九年級136名女生中,隨機抽取了20名女生,進行了1分鐘仰臥起坐測試,獲得數據如下:
收集數據:抽取20名女生的1分鐘仰臥起坐測試成績(個)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述數據:請你按如下分組整理、描述樣本數據,把下列表格補充完整:
范圍 |
|
|
|
|
|
|
|
人數 |
(說明:每分鐘仰臥起坐個數達到49個及以上時在中考體育測試中可以得到滿分)
(2)分析數據:樣本數據的平均數、中位數、滿分率如下表所示:
平均數 | 中位數 | 滿分率 |
46.8 | 47.5 |
|
得出結論:①估計該校九年級女生在中考體育測試中1分鐘“仰臥起坐”項目可以得到滿分的人數;
②該中心所在區縣的九年級女生的1分鐘“仰臥起坐”總體測試成績如下:
平均數 | 中位數 | 滿分率 |
45.3 | 49 |
|
請你結合該校樣本測試成績和該區縣總體測試成績,為該校九年級女生的1分鐘“仰臥起坐”達標情況做一下評估.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com