
【題目】(1)填寫下表,觀察被開方數(shù)![]() 的小數(shù)點(diǎn)與算術(shù)平方根
的小數(shù)點(diǎn)與算術(shù)平方根![]() 的小數(shù)點(diǎn)的移動規(guī)律:
的小數(shù)點(diǎn)的移動規(guī)律:
| 0.0016 | 0.16 | 16 | 1600 |
| 0.04 | 0.4 |
(2)根據(jù)你發(fā)現(xiàn)的規(guī)律填空:
①已知![]() ,則
,則![]() .
.
②已知![]() ,
,![]() ,則
,則![]() 是
是![]() 的 倍.
的 倍.
【答案】(1) 4,40 ;(2)①1.99;②10000
【解析】
(1)根據(jù)算術(shù)平方根的定義先求出每一個數(shù)的算術(shù)平方根,然后再根據(jù)小數(shù)點(diǎn)的變化進(jìn)行解答;
(2)①根據(jù)(1)中的規(guī)律對小數(shù)點(diǎn)移動進(jìn)行求解即可;
②根據(jù)(1)中的規(guī)律對小數(shù)點(diǎn)移動進(jìn)行求解即可.
(1)∵0.042=0.0016,∴![]() 0.04;
0.04;
同理:![]() 0.4,
0.4,
![]() 4;
4;
![]() 40
40
故答案為:4,40;
(2)①由表格可知,被開方數(shù)a 的小數(shù)點(diǎn)向右(或向左)每移動兩位時,![]() 的小數(shù)點(diǎn)向右(或向左)移動1位,
的小數(shù)點(diǎn)向右(或向左)移動1位,
根據(jù)此規(guī)律,可得![]() 1.99.
1.99.
故答案為:1.99;
②由表格可知,被開方數(shù)a 的小數(shù)點(diǎn)向右(或向左)每移動兩位時,![]() 的小數(shù)點(diǎn)向右(或向左)移動1位,已知
的小數(shù)點(diǎn)向右(或向左)移動1位,已知![]() 0.345,
0.345,![]() 34.5,則n是m的10000倍.
34.5,則n是m的10000倍.
故答案為:10000.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(1)化簡:[x(x2y2﹣xy)﹣2y(x2﹣x3y)]÷3x2y
(2)化簡求值:(x+2y)2﹣(x﹣2y)2﹣(x+2y)(x﹣2y)﹣4y2,其中y=1,x=![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,AE⊥BC于E,AF⊥CD于F,且∠EAF=60°,BE=2cm,DF=3cm,試求平行四邊形ABCD的周長及面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在△ABC中,AB=CB,∠ABC=90°,D為AB延長線上一點(diǎn),點(diǎn)E在BC邊上,且BE=BD,連結(jié)AE、DE、DC

①求證:△ABE≌△CBD;
②若∠CAE=30°,求∠BDC的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線y=k1x+b與x軸、y軸相交于P、Q兩點(diǎn),與y=![]() 的圖象相交于A(﹣2,m)、B(1,n)兩點(diǎn),連接OA、OB,給出下列結(jié)論:①k1k2<0;②m+
的圖象相交于A(﹣2,m)、B(1,n)兩點(diǎn),連接OA、OB,給出下列結(jié)論:①k1k2<0;②m+![]() n=0;③S△AOP=S△BOQ;④不等式k1x+b>
n=0;③S△AOP=S△BOQ;④不等式k1x+b>![]() 的解集是x<﹣2或0<x<1,其中正確的結(jié)論的序號是_____.
的解集是x<﹣2或0<x<1,其中正確的結(jié)論的序號是_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)y=kx+b(k、b為常數(shù),k≠0)的圖象與x軸、y軸分別交于A、B兩點(diǎn),且與反比例函數(shù)y=![]() (n為常數(shù),且n≠0)的圖象在第二象限交于點(diǎn)C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(n為常數(shù),且n≠0)的圖象在第二象限交于點(diǎn)C.CD⊥x軸,垂足為D,若OB=2OA=3OD=12.
(1)求一次函數(shù)與反比例函數(shù)的解析式;
(2)記兩函數(shù)圖象的另一個交點(diǎn)為E,求△CDE的面積;
(3)直接寫出不等式kx+b≤![]() 的解集.
的解集.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形ABCD中,M、N分別是BC、DC的中點(diǎn),AM=4,AN=3,且∠MAN=60°,則AB的長是_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】從三角形一個頂點(diǎn)引出一條射線與對邊相交,頂點(diǎn)與交點(diǎn)之間的線段把這個三角形分割成兩個小三角形,若分得的兩個小三角形中一個三角形為等腰三角形,另一個三角形的三個內(nèi)角與原來三角形的三個內(nèi)角分別相等,則稱這條線段叫做這個三角形的“等角分割線”.
例如,等腰直角三角形斜邊上的高就是這個等腰直角三角形的一條“等角分割線”.

(1)如圖1,在△ABC中,D是邊BC上一點(diǎn),若∠B=30°,∠BAD=∠C=40°,求證: AD為△ABC的“等角分割線”;
(2)如圖2,△ABC中,∠C=90°,∠B=30°;
①畫出△ABC的“等角分割線”,寫出畫法并說明理由;
②若BC=3,求出①中畫出的“等角分割線”的長度.
(3)在△ABC中,∠A=24°,若△ABC存在“等角分割線”CD,直接寫出所有符合要求的∠B的度數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
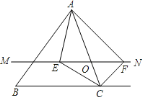
【題目】如圖,在![]() 中,點(diǎn)
中,點(diǎn)![]() 是
是![]() 邊上(端點(diǎn)除外)的一個動點(diǎn),過點(diǎn)
邊上(端點(diǎn)除外)的一個動點(diǎn),過點(diǎn)![]() 作直線
作直線![]() .設(shè)
.設(shè)![]() 交
交![]() 的平分線于點(diǎn)
的平分線于點(diǎn)![]() ,交
,交![]() 的外角平分線于點(diǎn)
的外角平分線于點(diǎn)![]() ,連接
,連接![]() 、
、![]() .那么當(dāng)點(diǎn)
.那么當(dāng)點(diǎn)![]() 運(yùn)動到何處時,四邊形
運(yùn)動到何處時,四邊形![]() 是矩形?并證明你的結(jié)論.
是矩形?并證明你的結(jié)論.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com