Question

【題目】如圖，二次函數y= x2+bx+c的圖象交x軸于A、D兩點，并經過B點，已知A點坐標是（2，0），B點坐標是（8，6）．
（1）求二次函數的解析式；
（2）求函數圖象的頂點坐標及D點的坐標；
（3）二次函數的對稱軸上是否存在一點C，使得△CBD的周長最小？若C點存在，求出C點的坐標；若C點不存在，請說明理由．

Answer 1

【答案】
（1）解：把A（2，0），B（8，6）代入y= x2+bx+c，得

，

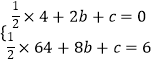解得： ，

∴二次函數的解析式為y= x2﹣4x+6

（2）解：由y= x2﹣4x+6= （x﹣4）2﹣2，得

二次函數圖象的頂點坐標為（4，﹣2）．

令y=0，得 x2﹣4x+6=0，

解得：x1=2，x2=6，

∴D點的坐標為（6，0）

（3）解：二次函數的對稱軸上存在一點C，使得△CBD的周長最小．

連接CA，如圖，

∵點C在二次函數的對稱軸x=4上，

∴xC=4，CA=CD，

∴△CBD的周長=CD+CB+BD=CA+CB+BD，

根據“兩點之間，線段最短”，可得

當點A、C、B三點共線時，CA+CB最小，

此時，由于BD是定值，因此△CBD的周長最小．

設直線AB的解析式為y=mx+n，

把A（2，0）、B（8，6）代入y=mx+n，得

，

解得： ，

∴直線AB的解析式為y=x﹣2．

當x=4時，y=4﹣2=2，

∴當二次函數的對稱軸上點C的坐標為（4，2）時，△CBD的周長最小．

【解析】（1）只需運用待定系數法就可求出二次函數的解析式；（2）只需運用配方法就可求出拋物線的頂點坐標，只需令y=0就可求出點D的坐標；（3）連接CA，由于BD是定值，使得△CBD的周長最小，只需CD+CB最小，根據拋物線是軸對稱圖形可得CA=CD，只需CA+CB最小，根據“兩點之間，線段最短”可得：當點A、C、B三點共線時，CA+CB最小，只需用待定系數法求出直線AB的解析式，就可得到點C的坐標．
【考點精析】根據題目的已知條件，利用確定一次函數的表達式和二次函數的性質的相關知識可以得到問題的答案，需要掌握確定一個一次函數，需要確定一次函數定義式y=kx+b（k不等于0）中的常數k和b．解這類問題的一般方法是待定系數法；增減性：當a>0時，對稱軸左邊，y隨x增大而減小；對稱軸右邊，y隨x增大而增大；當a<0時，對稱軸左邊，y隨x增大而增大；對稱軸右邊，y隨x增大而減小．