
【題目】如圖,在平面直角坐標系中,點![]() 坐標為
坐標為![]() ,點
,點![]() 是
是![]() 軸正半軸上一點,且
軸正半軸上一點,且![]() ,點
,點![]() 是
是![]() 軸上位于點
軸上位于點![]() 右側的一個動點,設點
右側的一個動點,設點![]() 的坐標為
的坐標為![]() .
.
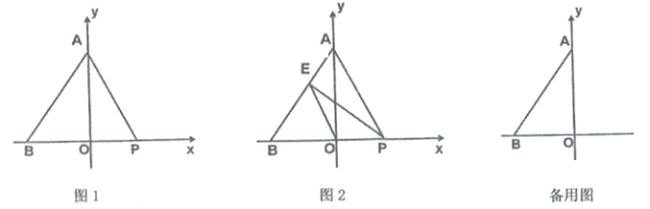
(1)點![]() 的坐標為( );
的坐標為( );
(2)當![]() 是等腰三角形時,求
是等腰三角形時,求![]() 點的坐標;
點的坐標;
(3)如圖2,過點![]() 作
作![]() 交線段
交線段![]() 于點
于點![]() ,連接
,連接![]() ,若點
,若點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,當點
,當點![]() 恰好落在直線
恰好落在直線![]() 上時,
上時,![]() .(直接寫出答案)
.(直接寫出答案)
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)利用勾股定理求出OA即可;
(2)分三種情況討論:①當![]() 時,②當
時,②當![]() 時,③當
時,③當![]() 時,分別進行計算即可;
時,分別進行計算即可;
(3)連接OA’, OA與PE交于點C,易得△OEA≌△OEA’,證明∠OA’E=∠OPC,求出OP=OA’=OA=4,易得∠BEO=∠PEO,作OG⊥EB于點G,OH⊥EP于點H,可得OG=OH,然后根據底邊上高相等的情況下,面積比等于底邊之比求出![]() ,再根據勾股定理構建方程即可求出BE.
,再根據勾股定理構建方程即可求出BE.
解:(1)∵![]()
![]() ,
,
∴OB=3,
∴OA=![]() ,
,
∴![]() ;
;
(2)當![]() 為等腰三角形時,分三種情況討論:
為等腰三角形時,分三種情況討論:
①當![]() 時,
時,
∵![]()
![]() ,
,
∴此時![]() ;
;
②當![]() 時,
時,
∵![]()
![]() ,
,
∴此時![]() ;
;
③當![]() 時,設P點坐標為(m,0),
時,設P點坐標為(m,0),
則:![]() ,
,
解得:![]() ,
,
∴此時![]() ;
;
(3)如圖,連接OA’, OA與PE交于點C,
∵點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() 在直線
在直線![]() 上,
上,
∴△OEA≌△OEA’,
∴∠OAE=∠OA’E,OA=OA’, ∠AEO=∠A’EO,
∵∠AEC=∠COP=90°,∠ACE=∠OCP,
∴∠OAE=∠OPC,
∴∠OA’E=∠OPC,
∴OP=OA’,
∴OP=OA=4,
∴BP=7,
∵∠AEO=∠A’EO,∠AEC=∠A’EB,
∴∠BEO=∠PEO,
作OG⊥EB于點G,OH⊥EP于點H,
則OG=OH,
∵![]() ,
,
∴![]() ,
,
設BE=3x,則EP=4x,
∵BE2+EP2=BP2,
∴![]() ,
,
解得:![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,AB=6cm,AC=8cm,動點P以3cm/s從點B出發向終點C運動;動點Q以1cm/s從點C出發向終點B運動,動點P,Q同時出發,以PQ為直徑在BC上方作半圓O,設運動時間為t(s).
(1)當t=1時,半圓O的半徑R=_______;
(2)當半圓O落在△ABC的內部(包括邊界)時,求t的取值范圍;
(3)當點P在Q的左邊時,過點P作PE//AB交半圓于點E.,求tan∠EAC的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,則下列結論:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正確的是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在二次函數![]() ,
,![]() 與
與![]() 的部分對應值如下表:
的部分對應值如下表:
| … |
|
|
|
| … |
| … |
|
|
|
| … |
則下列說法:①圖象經過原點;②圖象開口向下;③圖象經過點![]() ;④當
;④當![]() 時,
時,![]() 隨
隨![]() 的增大而增大;⑤方程
的增大而增大;⑤方程![]() 有兩個不相等的實數根.其中正確的是( )
有兩個不相等的實數根.其中正確的是( )
A. ①②③ B. ①③⑤ C. ①③④ D. ①④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在銳角三角形ABC中,AH是BC邊上的高,分別以AB,AC為一邊,向外作正方形ABDE和ACFG,連接CE,BG和EG,EG與HA的延長線交于點M,下列結論:①BG=CE;②BG⊥CE;③AM是△AEG的中線;④∠EAM=∠ABC,其中正確結論的個數是( )

A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC中,∠BAC=90°,AB=AC,點D為直線BC上一動點(點D不與B,C重合),以AD為邊在AD右側作正方形ADEF,連接CF.
(1)觀察猜想
如圖1,當點D在線段BC上時,
①BC與CF的位置關系為: .
②BC,CD,CF之間的數量關系為: ;(將結論直接寫在橫線上)
(2)數學思考
如圖2,當點D在線段CB的延長線上時,結論①,②是否仍然成立?若成立,請給予證明;若不成立,請你寫出正確結論再給予證明.
(3)拓展延伸
如圖3,當點D在線段BC的延長線上時,延長BA交CF于點G,連接GE.若已知AB=2![]() ,CD=
,CD=![]() BC,請求出GE的長.
BC,請求出GE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數![]() 和反比例函數
和反比例函數![]() ,
,![]() 與
與![]() 和
和![]() 的部分對應值如下表所示:
的部分對應值如下表所示:
| … |
| 4 | 8 | … |
| … | 1 |
| 4 | … |
| … | 4 | 2 |
| … |
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)指出當![]() 時,正比例函數圖像與反比例函數圖像的交點坐標;
時,正比例函數圖像與反比例函數圖像的交點坐標;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=﹣x2+bx+c與x軸交于點A(﹣1,0)和點B,與y軸交于C(0,3),直線y=![]() +m經過點C,與拋物線的另一交點為點D,點P是直線CD上方拋物線上的一個動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.
+m經過點C,與拋物線的另一交點為點D,點P是直線CD上方拋物線上的一個動點,過點P作PF⊥x軸于點F,交直線CD于點E,設點P的橫坐標為m.
(1)求拋物線解析式并求出點D的坐標;
(2)連接PD,△CDP的面積是否存在最大值?若存在,請求出面積的最大值;若不存在,請說明理由;
(3)當△CPE是等腰三角形時,請直接寫出m的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com