
【題目】某人身高![]() ,開(kāi)始時(shí)站在路燈下的影子長(zhǎng)為
,開(kāi)始時(shí)站在路燈下的影子長(zhǎng)為![]() ,然后他向路燈走近
,然后他向路燈走近![]() (指水平距離),此時(shí)他的影子長(zhǎng)與身高相等.求路燈高,以及開(kāi)始時(shí)他與路燈的水平距離.
(指水平距離),此時(shí)他的影子長(zhǎng)與身高相等.求路燈高,以及開(kāi)始時(shí)他與路燈的水平距離.
【答案】路燈高為![]() ,開(kāi)始時(shí)他與路燈的水平距離為
,開(kāi)始時(shí)他與路燈的水平距離為![]() .
.
【解析】
根據(jù)題意畫(huà)出圖形,進(jìn)而得出△E′F′D∽△ABD,△EFC∽△ABC,再利用相似三角性質(zhì)求出即可.
如圖所示:由題意可得:EF=E′F′=1.8m,FF′=3.6m,F′D=1.8m,FC=3.6m.
∵E′F′∥AB,EF∥AB,∴△E′F′D∽△ABD,△EFC∽△ABC,∴![]() ,設(shè)AB=x,BF′=y,則
,設(shè)AB=x,BF′=y,則![]() ,故
,故![]() ,解得:y=3.6,則x=5.4,故BF=3.6+3.6=7.2(m).
,解得:y=3.6,則x=5.4,故BF=3.6+3.6=7.2(m).
答:路燈高為5.4m,開(kāi)始時(shí)他與路燈的水平距離為7.2m.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
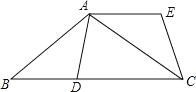
【題目】如圖,在△ABC 中,AB=AC.D 是 BC 上一點(diǎn),且 AD=BD.將△ABD 繞點(diǎn) A 逆時(shí)針旋轉(zhuǎn)得到△ACE.
(1)求證:AE∥BC;
(2)連結(jié) DE,判斷四邊形 ABDE 的形狀,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】有一個(gè)二次函數(shù)的圖象,三位同學(xué)分別說(shuō)出了它的一些特點(diǎn):
甲:對(duì)稱(chēng)軸為直線x=4
乙:與x軸兩個(gè)交點(diǎn)的橫坐標(biāo)都是整數(shù).
丙:與y軸交點(diǎn)的縱坐標(biāo)也是整數(shù),且以這三個(gè)點(diǎn)為頂點(diǎn)的三角形面積為3.請(qǐng)你寫(xiě)出滿足上述全部特點(diǎn)的一個(gè)二次函數(shù)解析式__________________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線y=-x2+bx+c的部分圖象如圖所示,A(1,0),B(0,3).
(1)求拋物線的解析式;
(2)結(jié)合函數(shù)圖象,寫(xiě)出當(dāng)y<3時(shí)x的取值范圍.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
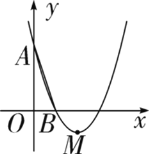
【題目】如圖,在平面直角坐標(biāo)系xOy中,已知拋物線y=x2+bx+C經(jīng)過(guò)A(0,3),B(1,0)兩點(diǎn),頂點(diǎn)為M.
(1)求b、C的值;
(2)將△OAB繞點(diǎn)B順時(shí)針旋轉(zhuǎn)90°后,點(diǎn)A落到點(diǎn)C的位置,該拋物線沿y軸上下平移后經(jīng)過(guò)點(diǎn)C,求平移后所得拋物線的表達(dá)式;
(3)設(shè)(2)中平移所得的拋物線與y軸的交點(diǎn)為A1,頂點(diǎn)為M1,若點(diǎn)P在平移后的拋物線上,且滿足△PMM1的面積是△PAA1面積的3倍,求點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
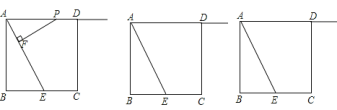
【題目】如圖,正方形![]() 的邊長(zhǎng)為
的邊長(zhǎng)為![]() ,
,![]() 是
是![]() 邊的中點(diǎn),點(diǎn)
邊的中點(diǎn),點(diǎn)![]() 在射線
在射線![]() 上,過(guò)
上,過(guò)![]() 作
作![]() 于
于![]() ,設(shè)
,設(shè)![]() .
.
(1)求證:![]() ;
;
(2)當(dāng)![]() 也是
也是![]() 邊中點(diǎn)時(shí),求
邊中點(diǎn)時(shí),求![]() 的值;
的值;
(3)若以![]() ,
,![]() ,
,![]() 為頂點(diǎn)的三角形也與
為頂點(diǎn)的三角形也與![]() 相似,試求
相似,試求![]() 的值;
的值;
(4)當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時(shí),設(shè)
重合時(shí),設(shè)![]() 交
交![]() 于點(diǎn)
于點(diǎn)![]() ,試判斷
,試判斷![]() 與
與![]() 的大小關(guān)系并說(shuō)明理由.
的大小關(guān)系并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB是⊙O的直徑,弦CD交AB于點(diǎn)P,AP=2,BP=6,∠APC=30°,則CD的長(zhǎng)為_______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知:如圖,在平面直角坐標(biāo)系xOy中,Rt△OCD的一邊OC在x軸上,∠C=90°,點(diǎn)D在第一象限,OC=3,DC=4,反比例函數(shù)的圖象經(jīng)過(guò)OD的中點(diǎn)A.
(1)求點(diǎn)A的坐標(biāo)及該反比例函數(shù)的解析式;
(2)若該反比例函數(shù)的圖象與Rt△OCD的另一邊DC交于點(diǎn)B,求過(guò)A、B兩點(diǎn)的直線的解析式.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在一個(gè)不透明的盒子里裝有黑、白兩種顏色的球共40只,這些球除顏色外其余完全相同.小穎做摸球?qū)嶒?yàn),攪勻后,她從盒子里隨機(jī)摸出一只球記下顏色后,再把球放回盒子中,不斷重復(fù)上述過(guò)程,下表是實(shí)驗(yàn)中的一組統(tǒng)計(jì)數(shù)據(jù):
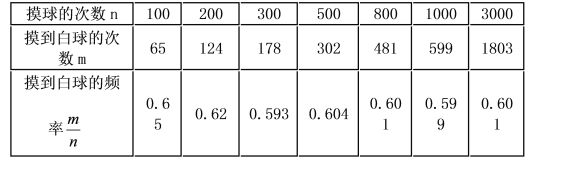
(1)請(qǐng)估計(jì):當(dāng)n很大時(shí),摸到白球的頻率將會(huì)接近______;(精確到0.1)
(2)若從盒子里隨機(jī)摸出一只球,則摸到白球的概率的估計(jì)值為______;
(3)試估算盒子里黑、白兩種顏色的球各有多少只?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com