
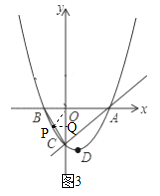
【題目】【本小題滿分11分】如圖,已知拋物線![]() 的頂點D的坐標為(1,
的頂點D的坐標為(1,![]() ),且與x軸交于A、B兩點,與y軸交于C點,A點的坐標為(4,0).P點是拋物線上的一個動點,且橫坐標為m.
),且與x軸交于A、B兩點,與y軸交于C點,A點的坐標為(4,0).P點是拋物線上的一個動點,且橫坐標為m.
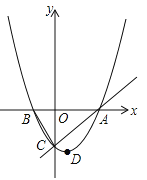
(l)求拋物線所對應的二次函數的表達式;
(2)若動點P滿足∠PAO不大于45°,求P點的橫坐標m的取值范圍;
(3)當P點的橫坐標![]() 時,過p點作y軸的垂線PQ,垂足為Q.問:是否存在P點,使∠QPO=∠BCO?若存在,請求出P點的坐標;若不存在,請說明理由.
時,過p點作y軸的垂線PQ,垂足為Q.問:是否存在P點,使∠QPO=∠BCO?若存在,請求出P點的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)﹣4≤m≤0;(3)P(
;(2)﹣4≤m≤0;(3)P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() ).
).
【解析】
試題(1)根據函數值相等的點關于對稱軸對稱,可得B點坐標,根據待定系數法,可得函數解析式;
(2)根據等腰直角三角形的性質,可得射線AC、AD,根據角越小角的對邊越小,可得PA在在射線AC與AD之間,根據解方程組,可得E點的橫坐標,根據E、C點的橫坐標,可得答案;
(3)分兩種情況,P在第二象限和P在第三象限討論.
試題解析:(1)由A、B點的函數值相等,得:A、B關于對稱軸對稱.A(4,0),對稱軸是x=1,得:B(﹣2,0).將A、B、D點的坐標代入解析式,得: ,解得:
,解得: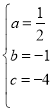 ,拋物線所對應的二次函數的表達式
,拋物線所對應的二次函數的表達式![]() ;
;
(2)如圖1作C點關于原點的對稱點D,OC=OD=OA=4,∠OAC=∠DAO=45°,AP在射線AC與AD之間,∠PAO<45°,直線AD的解析式為![]() ,聯立AD于拋物線,得:
,聯立AD于拋物線,得: ,解得x=﹣4或x=4,∵E點的橫坐標是﹣4,C點的橫坐標是0,P點的橫坐標的取值范圍是﹣4≤m≤0;
,解得x=﹣4或x=4,∵E點的橫坐標是﹣4,C點的橫坐標是0,P點的橫坐標的取值范圍是﹣4≤m≤0;

(3)存在P點,使∠QPO=∠BCO,①若點P在第二象限,如圖2,設P(a,![]() ),由∠QPO=∠BCO,∠PQO=CBO=90°,∴△PQO∽△COB,∴
),由∠QPO=∠BCO,∠PQO=CBO=90°,∴△PQO∽△COB,∴![]() ,即
,即![]() =
=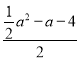 ,化簡,得
,化簡,得![]() ,解得
,解得![]() 或
或![]() (不符合題意,舍),∴
(不符合題意,舍),∴![]() =
=![]() ,∴P點坐標為(
,∴P點坐標為(![]() ,
,![]() );
);
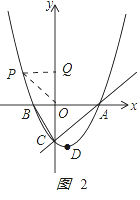
②若點P在第三象限,如圖3,由△PQO∽△COB,∴PQ:CO=OQ:OB,∵B(-2,0),C(0,-4),∴PQ=2QO,∴點P坐標為(m,![]() ),代入
),代入![]() ,得:
,得:![]() ,解得:
,解得:![]() ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴![]() =
=![]() ,∴P的坐標為(
,∴P的坐標為(![]() ,
,![]() );
);
∴滿足條件的點為P(![]() ,
,![]() )或P(
)或P(![]() ,
,![]() ).
).


科目:初中數學 來源: 題型:
【題目】已知:如圖1,OM是∠AOB的平分線,點C在OM上,OC=5,且點C到OA的距離為3.過點C作CD⊥OA,CE⊥OB,垂足分別為D、E,易得到結論:OD+OE=_________;

(1)把圖1中的∠DCE繞點C旋轉,當CD與OA不垂直時(如圖2),上述結論是否成立?并說明理由;
(2)把圖1中的∠DCE繞點C旋轉,當CD與OA的反向延長線相交于點D時:
①請在圖3中畫出圖形;
②上述結論還成立嗎?若成立,請給出證明;若不成立,請直接寫出線段OD、OE之間的數量關系,不需證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線![]() 交
交![]() 軸于點
軸于點![]() ,交
,交![]() 軸于點
軸于點![]() ,以
,以![]() 為邊作正方形
為邊作正方形![]() ,請解決下列問題:
,請解決下列問題:
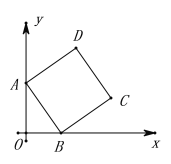
(1)求點![]() 和點
和點![]() 的坐標;
的坐標;
(2)求直線![]() 的解析式;
的解析式;
(3)在直線![]() 上是否存在點
上是否存在點![]() ,使
,使![]() 為等腰三角形?若存在,請直接寫出點
為等腰三角形?若存在,請直接寫出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象拋物線G經過(﹣5,0),(0,![]() ),(1,6)三點,直線l的解析式為y=2x﹣3
),(1,6)三點,直線l的解析式為y=2x﹣3
(1)求拋物線G的函數解析式;
(2)求證:拋物線G與直線L無公共點;
(3)若與l平行的直線y=2x+m與拋物線G只有一個公共點P,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是反比例函數![]() 的圖象的一個分支.
的圖象的一個分支.
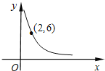
![]() 比例系數
比例系數![]() 的值是________;
的值是________;
![]() 寫出該圖象的另一個分支上的
寫出該圖象的另一個分支上的![]() 個點的坐標:________、________;
個點的坐標:________、________;
![]() 當
當![]() 在什么范圍取值時,
在什么范圍取值時,![]() 是小于
是小于![]() 的正數?
的正數?
![]() 如果自變量
如果自變量![]() 取值范圍為
取值范圍為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商家獨家銷售具有地方特色的某種商品,每件進價為40元.經過市場調查,一周的銷售量y件與銷售單價x(x≥50)元/件的關系如下表:
銷售單價x(元/件) | … | 55 | 60 | 70 | 75 | … |
一周的銷售量y(件) | … | 450 | 400 | 300 | 250 | … |
(1)直接寫出y與x的函數關系式: .
(2)設一周的銷售利潤為S元,請求出S與x的函數關系式,并確定當銷售單價在什么范圍內變化時,一周的銷售利潤隨著銷售單價的增大而增大?
(3)雅安地震牽動億萬人民的心,商家決定將商品一周的銷售利潤全部寄往災區,在商家購進該商品的貸款不超過10000元情況下,請你求出該商家最大捐款數額是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
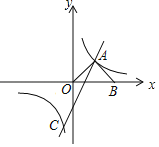
【題目】如圖,在平面直角坐標系中,直線y1=2x﹣2與雙曲線y2=![]() 交于A、C兩點,AB⊥OA交x軸于點B,且OA=AB.
交于A、C兩點,AB⊥OA交x軸于點B,且OA=AB.
(1)求雙曲線的解析式;
(2)求點C的坐標,并直接寫出y1<y2時x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
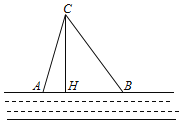
【題目】在一條東西走向河的一側有一村莊C,河邊原有兩個取水點A,B,其中AB=AC,由于某種原因,由C到A的路現在已經不通,該村為方便村民取水決定在河邊新建一個取水點H(A、H、B在同一條直線上),并新修一條路CH,測得CB=2.5千米,CH=2千米,HB=1.5千米.
(1)問CH是否為從村莊C到河邊的最近路?請通過計算加以說明;
(2)求原來的路線AC的長.(精確到0.01)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com