
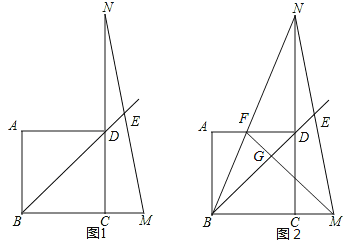
【題目】如圖1,在正方形ABCD中,延長BC至M,使BM=DN,連接MN交BD延長線于點E.
(1)求證:BD+2DE=![]() BM.
BM.
(2)如圖2,連接BN交AD于點F,連接MF交BD于點G.若AF:FD=1:2,且CM=2,則線段DG= .
【答案】(1)證明見解析;(2)![]() .
.
【解析】試題(1)根據結論可以猜想:要想解決問題需要把BD+2DE和BM轉化到等腰直角三角形中去,因此想到過點M作BM的垂線與BD 的延長線交于點P,然后利用全等三角形的性質證明DE=PE即可證出結論;(2)由AB//CN可得:![]() ,所以DN=BM=2AB=2BC,又CM=2,所以BC=AD=CM=2,所以BD=
,所以DN=BM=2AB=2BC,又CM=2,所以BC=AD=CM=2,所以BD=![]() ,FD=
,FD=![]() ,由AD//BM可得:
,由AD//BM可得:![]() ,所以
,所以![]() ,因為BD=
,因為BD=![]() ,所以DG=
,所以DG=![]() .
.
試題解析:(1)證明:過點M作NP![]() BM,交BD 的延長線交于點P,
BM,交BD 的延長線交于點P,
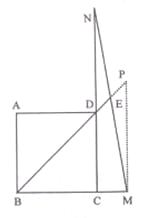
因為四邊形ABCD是正方形,所以∠BCD =90°,∠DBC=∠BDC=45°,
所以PM∥CN,所以∠N=∠EMP,∠BDC=∠MPB=45°,
所以∠DBC=∠MPB,所以BM=MP,又因為BM=DN,所以DN=MP,
又因為∠N=∠EMP,∠NED=∠MEP,所以△NDE≌△MPE,所以DE=EP
由勾股定理可得:BP=![]() BM,即BD+2DE=
BM,即BD+2DE=![]() BM
BM
(2)DG=![]()


科目:初中數學 來源: 題型:
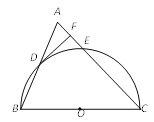
【題目】(9分)如圖,△ABC為等腰三角形,AC=BC,以邊BC為直徑的半圓與邊AB,AC分別交于D,E兩點,過點D作DF⊥AC,垂足為點F.
(1)判斷DF與⊙O的位置關系,并證明你的結論;
(2)若BC=9,EF=1,求DF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知第一象限內的點A在反比例函數y=![]() 的圖象上,第二象限內的點B在反比例函數y=
的圖象上,第二象限內的點B在反比例函數y=![]() 的圖象上,且OA⊥OB,cosA=
的圖象上,且OA⊥OB,cosA=![]() ,則k的值為( )
,則k的值為( )

A. -3 B. -6 C. -4 D. -![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在一個長方形休閑廣場的四角都設計一塊半徑相同的四分之一圓形的花壇,若圓形的半徑為![]() 米,廣場的長為
米,廣場的長為![]() 米,寬為
米,寬為![]() 米.
米.
(1)請列式表示花壇的面積和廣場空地的面積;
(2)若休閑廣場的長為500米,寬為200米,圓形花壇的半徑為20米,求廣場空地的面積;(計算結果保留![]() ;
;
(3)在(2)的情況下,若![]() 取3.14,求休閑廣場的綠化率是多少?
取3.14,求休閑廣場的綠化率是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了落實黨的“精準扶貧”政策,A、B兩城決定向C、D兩鄉運送肥料以支持農村生產,已知A、B兩城共有肥料500噸,其中A城肥料比B城少100噸,從A城往C、D兩鄉運肥料的費用分別為20元/噸和25元/噸;從B城往C、D兩鄉運肥料的費用分別為15元/噸和24元/噸.現C鄉需要肥料240噸,D鄉需要肥料260噸.
(1)A城和B城各有多少噸肥料?
(2)設從A城運往C鄉肥料x噸,總運費為y元,求出最少總運費.
(3)由于更換車型,使A城運往C鄉的運費每噸減少a(0<a<6)元,這時怎樣調運才能使總運費最少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知含字母a,b的代數式是:3[a2+2(b2+ab﹣2)]﹣3(a2+2b2)﹣4(ab﹣a﹣1)
(1)化簡代數式;
(2)小紅取a,b互為倒數的一對數值代入化簡的代數式中,恰好計算得代數式的值等于0,那么小紅所取的字母b的值等于多少?
(3)聰明的小剛從化簡的代數式中發現,只要字母b取一個固定的數,無論字母a取何數,代數式的值恒為一個不變的數,那么小剛所取的字母b的值是多少呢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、B分別為數軸上的兩點,A點對應的數為﹣20,B點對應的數為100.
![]()
(1)請寫出與A,B兩點距離相等的點M所對應的數 .
(2)現有一只電子螞蟻P從B點出發,以6單位/秒的速度向左運動,同時另一只電子螞蟻Q恰好從A點出發,以4單位/秒的速度向右運動,x秒后兩只電子螞蟻在數軸上的C點相遇,請列方程求出x,并指出點C表示的數.
(3)若當電子螞蟻P從B點出發時,以6單位/秒的速度向左運動,同時另一只電子螞蟻Q恰好從A點出發,以4單位/秒的速度也向左運動,y秒后兩只電子螞蟻在數軸上的D點相遇,請列方程求出y并指出點D表示的數.
查看答案和解析>>
科目:初中數學 來源: 題型:
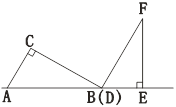
【題目】兩個三角板ABC,DEF按如圖所示的位置擺放,點B與點D重合,邊AB與邊DE在同一條直線上(假設圖形中所有的點、線都在同一平面內),其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=4 cm.現固定三角板DEF,將三角板ABC沿射線DE方向平移,當點C落在邊EF上時停止運動.設三角板平移的距離為![]() (cm),兩個三角板重疊部分的面積為
(cm),兩個三角板重疊部分的面積為![]() (cm2).
(cm2).
(1)當點C落在邊EF上時,![]() =________cm;
=________cm;
(2)求![]() 關于
關于![]() 的函數表達式,并寫出自變量
的函數表達式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(3)設邊BC的中點為點M,邊DF的中點為點N,直接寫出在三角板平移過程中,點M與點N之間距離的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com