
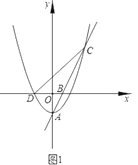
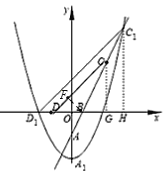
【題目】如圖1,拋物線![]() 的頂點為點
的頂點為點![]() ,與
,與![]() 軸的負半軸交于點
軸的負半軸交于點![]() ,直線
,直線![]() 交拋物線W于另一點
交拋物線W于另一點![]() ,點
,點![]() 的坐標為
的坐標為![]() .
.
(1)求直線![]() 的解析式;
的解析式;
(2)過點![]() 作
作![]() 軸,交
軸,交![]() 軸于點
軸于點![]() ,若
,若![]() 平分
平分![]() ,求拋物線W的解析式;
,求拋物線W的解析式;
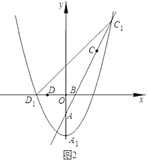
(3)若![]() ,將拋物線W向下平移
,將拋物線W向下平移![]() 個單位得到拋物線
個單位得到拋物線![]() ,如圖2,記拋物線
,如圖2,記拋物線![]() 的頂點為
的頂點為![]() ,與
,與![]() 軸負半軸的交點為
軸負半軸的交點為![]() ,與射線
,與射線![]() 的交點為
的交點為![]() .問:在平移的過程中,
.問:在平移的過程中,![]() 是否恒為定值?若是,請求出
是否恒為定值?若是,請求出![]() 的值;若不是,請說明理由.
的值;若不是,請說明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 恒為定值
恒為定值![]() .
.
【解析】
(1)由拋物線解析式可得頂點A坐標為(0,-2),利用待定系數法即可得直線AB解析式;
(2)如圖,過點![]() 作
作![]() 于
于![]() ,根據角平分線的性質可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可證明
,根據角平分線的性質可得BE=BN,由∠BND=∠CED=90°,∠BND=∠CDE可證明![]() ,設BE=x,BD=y,根據相似三角形的性質可得CE=2x,CD=2y,根據勾股定理由得y與x的關系式,即可用含x的代數式表示出C、D坐標,代入y=ax2-2可得關于x、a的方程組,解方程組求出a值即可得答案;
,設BE=x,BD=y,根據相似三角形的性質可得CE=2x,CD=2y,根據勾股定理由得y與x的關系式,即可用含x的代數式表示出C、D坐標,代入y=ax2-2可得關于x、a的方程組,解方程組求出a值即可得答案;
(3)過點![]() 作
作![]() 于點
于點![]() ,根據平移規律可得拋物線W1的解析式為y=
,根據平移規律可得拋物線W1的解析式為y=![]() x2-2-m,設點
x2-2-m,設點![]() 的坐標為(t,0)(t<0),代入y=
的坐標為(t,0)(t<0),代入y=![]() x2-2-m可得2+m=
x2-2-m可得2+m=![]() t2,即可的W1的解析式為y=
t2,即可的W1的解析式為y=![]() x2-
x2-![]() t2,聯立直線BC解析式可用含t的代數式表示出點C1的坐標,即可得
t2,聯立直線BC解析式可用含t的代數式表示出點C1的坐標,即可得![]() ,可得∠
,可得∠![]() ,根據拋物線W的解析式可得點D坐標,聯立直線BC與拋物線W的解析式可得點C、A坐標,即可求出CG、DG的長,可得CG=DG,∠CDG=∠
,根據拋物線W的解析式可得點D坐標,聯立直線BC與拋物線W的解析式可得點C、A坐標,即可求出CG、DG的長,可得CG=DG,∠CDG=∠![]() ,即可證明
,即可證明![]() ,可得
,可得![]() ,
,![]() ,由∠CDG=45°可得BF=DF,根據等腰三角形的性質可求出DF的長,利用勾股定理可求出CD的長,即可求出CF的長,根據三角函數的定義即可得答案.
,由∠CDG=45°可得BF=DF,根據等腰三角形的性質可求出DF的長,利用勾股定理可求出CD的長,即可求出CF的長,根據三角函數的定義即可得答案.
(1)∵拋物線W:![]() 的頂點為點
的頂點為點![]() ,
,
∴點![]() ,
,
設直線![]() 解析式為
解析式為![]() ,
,
∵B(1,0),
∴![]() ,
,
解得:![]() ,
,
∴拋物線解析式為:![]() .
.
(2)如圖,過點![]() 作
作![]() 于
于![]() ,
,
∵![]() 平分,
平分,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
設![]() ,則
,則![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴點![]() ,點
,點![]() ,
,
∴點![]() ,點
,點![]() 是拋物線W:
是拋物線W:![]() 上的點,
上的點,
∴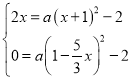 ,
,
∵x>0,
∴![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴拋物線解析式為:![]() .
.
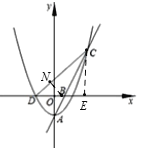
(3)![]() 恒為定值,理由如下:
恒為定值,理由如下:
如圖,過點![]() 作
作![]() 軸于H,過點
軸于H,過點![]() 作
作![]() 軸G,過點
軸G,過點![]() 作
作![]() 于點
于點![]() ,
,
∵a=![]() ,
,
∴拋物線W的解析式為y=![]() x2-2,
x2-2,
∵將拋物線W向下平移m個單位,得到拋物線![]() ,
,
∴拋物線![]() 的解析式為:
的解析式為:![]() ,
,
設點![]() 的坐標為
的坐標為![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴拋物線![]() 的解析式為:
的解析式為:![]() ,
,
∵拋物線![]() 與射線
與射線![]() 的交點為
的交點為![]() ,
,
∴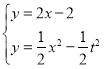 ,
,
解得: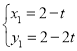 ,
,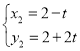 (不合題意舍去),
(不合題意舍去),
∴點![]() 的坐標
的坐標![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,且
,且![]() 軸,
軸,
![]() ,
,
∵![]() 與
與![]() 軸交于點
軸交于點![]() ,
,
∴點![]() ,
,
∵![]() 與
與![]() 交于點
交于點![]() ,點
,點![]() ,
,
∴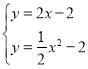 ,
,
解得:![]() 或
或![]() ,
,
∴點![]() ,A(0,-2),
,A(0,-2),
∴![]() ,
,
∴![]() ,且
,且![]() 軸,
軸,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵點![]() ,點
,點![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 恒為定值.
恒為定值.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
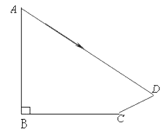
【題目】如圖:學校旗桿附近有一斜坡.小明準備測量學校旗桿AB的高度,他發現當斜坡正對著太陽時,旗桿AB的影子恰好落在水平地面和斜坡的坡面上,此時小明測得水平地面上的影長BC=16米,斜坡坡面上的影長CD=10米,太陽光線AD與水平地面成30°角,斜坡CD與水平地面BC成30°的角,求旗桿AB的高度(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解下列一元二次方程.
(1)(x+3)2﹣25=0;
(2)3(1+x)2=27;
(3)x2﹣4x+6=0;
(4)(x﹣1)(x+3)=12;
(5)3(x﹣2)2=x(x﹣2).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,平面直角坐標系中,直線y=-x+6交x軸于點A,交y軸于點B,點C為OB上一點,連接AC,且![]() ;
;
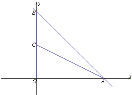
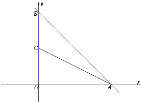
(1)求C點坐標;
(2)D為OC上一點,連接AD并延長至點E,連接OE、CE,取AE中點F,連接BF、OF,當F在第一象限時,求![]() 的值;
的值;
(3)在(2)的條件下,將射線AC延AE翻折交OE于點P,連接BP,過O作OH⊥AE于H,若AD=4FH,![]() ,求直線PB的解析式.
,求直線PB的解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場要經營一種新上市的文具,進價為![]() 元
元![]() 件.試營銷階段發現:當銷售單價是
件.試營銷階段發現:當銷售單價是![]() 元時,每天的銷售量為
元時,每天的銷售量為![]() 件;銷售單價每上漲
件;銷售單價每上漲![]() 元,每天的銷售量就減少
元,每天的銷售量就減少![]() 件.
件.
(1)寫出商場銷售這種文具,每天所得的銷售利潤![]() (元)與銷售單價
(元)與銷售單價![]() (元)之間的函數關系式.
(元)之間的函數關系式.
(2)當銷售單價定為多少元時,該文具每天的銷售利潤最大?最大利潤為多少元?
(3)商場的營銷部結合上述情況,提出了![]() ,
,![]() 兩種營銷方案:
兩種營銷方案:
方案![]() :該文具的銷售單價高于進價,但不超過
:該文具的銷售單價高于進價,但不超過![]() 元;
元;
方案![]() :每天銷售量不少于
:每天銷售量不少于![]() 件,且每件文具的利潤至少為
件,且每件文具的利潤至少為![]() 元.
元.
請比較哪種方案的最大利潤更高,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() 的坐標為
的坐標為![]() ,點
,點![]() 的變換點
的變換點![]() 的坐標定義如下:當
的坐標定義如下:當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() ;當
;當![]() 時,點
時,點![]() 的坐標為
的坐標為![]() .
.
(1)點![]() 的變換點
的變換點![]() 的坐標是_________;點
的坐標是_________;點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,
,![]() ,則
,則![]() __________
__________![]() ;
;
(2)若點![]() 是函數
是函數![]() 圖象上的一點,點
圖象上的一點,點![]() 的變換點為
的變換點為![]() ,連接
,連接![]() ,求線段
,求線段![]() 長的取值范圍;
長的取值范圍;
(3)已知拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() (點
(點![]() 在點
在點![]() 的左側),頂點為
的左側),頂點為![]() .點
.點![]() 在拋物線
在拋物線![]() 上,點
上,點![]() 的變換點為
的變換點為![]() .若點
.若點![]() 恰好在拋物線的對稱軸上,且四邊形
恰好在拋物線的對稱軸上,且四邊形![]() 是菱形,求
是菱形,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD是角平分錢,點E在AC上,且∠EAD=∠ADE.

(1)求證:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了調查學生對垃圾分類及投放知識的了解情況,從甲、乙兩校各隨機抽取40名學生進行了相關知識測試,獲得了他們的成績(百分制),并對數據(成績)進行了整理、描述和分析.下面給出了部分信息.
a.甲、乙兩校40名學生成績的頻數分布統計表如下:
成績x 學校 |
|
|
|
|
|
甲 | 4 | 11 | 13 | 10 | 2 |
乙 | 6 | 3 | 15 | 14 | 2 |
(說明:成績80分及以上為優秀,70~79分為良好,60~69分為合格,60分以下為不合格)
b.甲校成績在![]() 這一組的是:
這一組的是:
70 70 70 71 72 73 73 73 74 75 76 77 78
c.甲、乙兩校成績的平均分、中位數、眾數如下:
學校 | 平均分 | 中位數 | 眾數 |
甲 | 74.2 | n | 85 |
乙 | 73.5 | 76 | 84 |
根據以上信息,回答下列問題:
(1)寫出表中n的值;
(2)在此次測試中,某學生的成績是74分,在他所屬學校排在前20名,由表中數據可知該學生是_____________校的學生(填“甲”或“乙”),理由是__________;
(3)假設乙校800名學生都參加此次測試,估計成績優秀的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果店在兩周內,將標價為10元/斤的某種水果,經過兩次降價后的價格為8.1元/斤,并且兩次降價的百分率相同.
(1)求該種水果每次降價的百分率;
(2)從第一次降價的第1天算起,第![]() 天(
天(![]() 為整數)的售價、銷量及儲存和損耗費用的相關信息如表所示.
為整數)的售價、銷量及儲存和損耗費用的相關信息如表所示.
時間 |
|
|
售價(元/斤) | 第1次降價后的價格 | 第2次降價后的價格 |
銷量(斤) |
|
|
儲存和損耗費用(元) |
|
|
已知該種水果的進價為4.1元/斤,設銷售該水果第![]() (天)的利潤為
(天)的利潤為![]() (元),求
(元),求![]() 與
與![]() (
(![]() )之間的函數解析式,并求出第幾天時銷售利潤最大.
)之間的函數解析式,并求出第幾天時銷售利潤最大.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com