
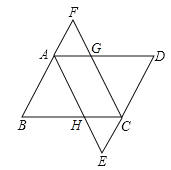
【題目】如圖,四邊形ABCD為平行四邊形,∠BAD和∠BCD的平分線AE,CF分別交DC,BA的延長線于點E,F,交邊BC,AD于點H,G.
(1)求證:四邊形AECF是平行四邊形.
(2)若AB=5,BC=8,求AF+AG的值.
【答案】(1)證明見解析;(2)6.
【解析】
(1)由平行四邊形的性質,結合角平分線的定義可證得AE∥CF,結合AF∥CE,可證得結論;
(2)由條件可證得△DCG∽△AFG,利用相似三角形的性質可求得DG與AG的關系,結合條件可求得AG的長,從而可求得答案.
(1)證明:∵四邊形ABCD為平行四邊形,
∴AD∥BC,∠BAD=∠BCD,
∵AE、CF分別平分∠BAD∠BCD,
∴∠BCG=∠CGD=∠HAD,
∴AE∥CF,
∵AF∥CE,
∴四邊形AECF是平行四邊形;
(2)解:由(1)可知∠BCF=∠DCF=∠F,
∴BF=BC=AD=8,
∵AB=CD=5,
∴AF=BF﹣AB=3,
∵BF∥DE,
∴∠DCG=∠F,∠D=∠FAG,
∴△DCG∽△AFG,
∴![]() =
=![]() ,
,
∴DG=![]() AG,
AG,
∴AD=AG+DG=![]() AG=8,
AG=8,
∴AG=3,
∴AF+AG=3+3=6.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:初中數學 來源: 題型:
【題目】問題探究:
如圖1,△ACB和△DCE均為等邊三角形,點A、D、E在同一直線上,連接BE.
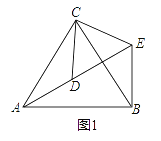
(1)證明:AD=BE;
(2)求∠AEB的度數.
問題變式:
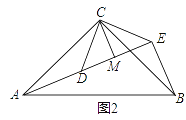
(3)如圖2,△ACB和△DCE均為等腰直角三角形,∠ACB=∠DCE=90°,點A、D、E在同一直線上,CM為△DCE中DE邊上的高,連接BE.(Ⅰ)請求出∠AEB的度數;(Ⅱ)判斷線段CM、AE、BE之間的數量關系,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
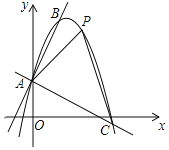
【題目】如圖,一個二次函數的圖象經過點A(0,1),它的頂點為B(1,3).
(1)求這個二次函數的表達式;
(2)過點A作AC⊥AB交拋物線于點C,點P是直線AC上方拋物線上的一點,當△APC面積最大時,求點P的坐標和△APC的面積最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市銷售A,B兩款保溫杯,已知B款保溫杯的銷售單價比A款保溫杯多10元,用480元購買B款保溫杯的數量與用360元購買A款保溫杯的數量相同.
(1)A,B兩款保溫杯的銷售單價各是多少元?
(2)由于需求量大,A,B兩款保溫杯很快售完,該超市計劃再次購進這兩款保溫杯共120個,且A款保溫杯的數量不少于B保溫杯的2倍,A保溫杯的售價不變,B款保溫杯的銷售單價降低10%,兩款保溫杯的進價每個均為20元,應如何進貨才能使這批保溫杯的銷售利潤最大,最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“六一”兒童節前,玩具商店根據市場調查,用2500元購進一批兒童玩具,上市后很快脫銷,接著又用4500元購進第二批這種玩具,所購數量是第一批數量的1.5倍,但每套進價多了10元.第一、二批玩具每套的進價分別是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2020年3月,我國湖北省A、B兩市遭受嚴重新冠肺炎影響,鄰近縣市C、D獲知A、B兩市分別急需救災物資200噸和300噸的消息后,決定調運物資支援災區.已知C市有救災物資240噸,D市有救災物資260噸,現將這些救災物資全部調往A、B兩市.已知從C市運往A、B兩市的費用分別為每噸20元和25元,從D市運往往A、B兩市的費用分別為每噸15元和30元,設從D市運往B市的救災物資為x噸.
(1)設C、D兩市的總運費為w元,求w與x之間的函數關系式,并寫出自變量x的取值范圍;
(2)經過當地政府的大力支持,從D市到B市的運輸時間縮短了,運費每噸減少m元(m>0),其余路線運費不變.若C、D兩市的總運費的最小值不小于10320元,求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小王計劃批發“山東大櫻桃”和“泰國榴蓮”兩個品種的水果共120斤,櫻桃和榴蓮的批發價分別為32元/斤和40元/斤.設購買了櫻桃x斤![]() .
.
(1)若小王批發這兩種水果正好花費了4400元,那么小王分別購買了多少斤櫻桃和榴蓮?填寫下表,并列方程求解;
品種 | 批發價(元) | 購買斤數 | 小王應付的錢數(元) |
櫻桃 | 32 | x | |
榴蓮 | 40 |
(2)設小王購買兩種水果的總花費為y元,試寫出y與x之間的函數表達式.
(3)若要求所批發的榴蓮的斤數不少于櫻桃斤數的2倍,那么購買櫻桃的數量為多少時,可使小王的總花費最少?這個最少花費是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
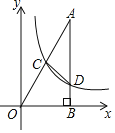
【題目】如圖,已知在平面直角坐標系xOy中,Rt△OAB的直角頂點B在x軸的正半軸上,點A在第一象限,反比例函數y=![]() (x>0)的圖象經過OA的中點C.交AB于點D,連結CD.若△ACD的面積是2,則k的值是_____.
(x>0)的圖象經過OA的中點C.交AB于點D,連結CD.若△ACD的面積是2,則k的值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠A=∠C=90°,DE,BF分別平分∠ADC,∠ABC,并交線段AB,CD于點E,F(點E,B不重合).在線段BF上取點M,N(點M在BN之間),使BM=2FN.當點P從點D勻速運動到點E時,點Q恰好從點M勻速運動到點N.記QN=x,PD=y,已知![]() ,當Q為BF中點時,
,當Q為BF中點時,![]() .
.
(1)判斷DE與BF的位置關系,并說明理由;
(2)求DE,BF的長;
(3)若AD=6.①當DP=DF時,通過計算比較BE與BQ的大小關系;②連結PQ,當PQ所在直線經過四邊形ABCD的一個頂點時,求所有滿足條件的x的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com