
【題目】已知關于![]() 的方程x2-(2k+1)x+4k-2=0
的方程x2-(2k+1)x+4k-2=0
(1)求證:不論k取何值,這個方程總有實數根
(2)若等腰△ABC一邊長a=4,另兩邊長b,c恰好是這個方程的兩根,求△ABC的周長.
【答案】(1)證明見解析;(2)10.
【解析】(1)根據方程各項的系數利用根的判別式即可得出=(2k-3)2≥0,此題得證;
(2)當a為底時,則b、c為腰,根據兩根相等得出k的值;當a為腰時,則b、c中有一個的值也等于4,將其代入方程求出k的值;再根據根與系數的關系求出a+b的值,進而可求出三角形的周長.
(1)證明:∵在方程x2-(2k+1)x+4k-2=0中,
△=[-(2k+1)]2-4(4k-2)=4k2-12k+9=(2k-3)2≥0,
∴不論k取什么實數值,這個方程總有實數根;
(2)解:當a為底邊時,b=c,
∴△=(2k-3)2=0,解得:k=![]() ,
,
∴b+c=2k+1=4=a,
∴此種情況不合適;
當a為腰時,將x=4代入原方程得:16-4(2k+1)+4k-2=0,
解得:k=![]() .
.
∴b+c=2k+1=6,
∴△ABC的周長=a+b+c=4+6=10.


科目:初中數學 來源: 題型:
【題目】如圖,已知等邊三角形ABC的邊長為2,E、F、G分別是邊AB、BC、CA的點,且AE=BF=CG,設△EFG的面積為y,AE的長為x,則y與x的函數圖象大致是( )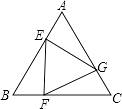
A.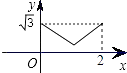
B.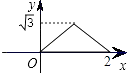
C.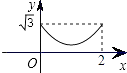
D.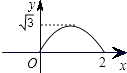
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖甲,在△ABC中,∠ACB=90°,AC=4cm,BC=3cm.如果點P由點B出發沿BA方向向點A勻速運動,同時點Q由點A出發沿AC方向向點C勻速運動,它們的速度均為1cm/s.連接PQ,設運動時間為t(s)(0<t<4),解答下列問題: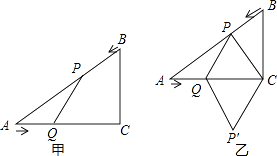
(1)設△APQ的面積為S,當t為何值時,S取得最大值?S的最大值是多少?
(2)如圖乙,連接PC,將△PQC沿QC翻折,得到四邊形PQP′C,當四邊形PQP′C為菱形時,求t的值;′
(3)當t為何值時,△APQ是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】□ABCD中,E、F是對角線BD上不同的兩點,下列條件中,不能得出四邊形AECF一定為平行四邊形的是( )
A. BE=DF B. AE=CF C. AF//CE D. ∠BAE=∠DCF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
若A、B、C為數軸上三點,若點C到A的距離是點C到B的距離2倍,我們就稱點C是(A,B)的妙點.
例如,如圖1,點A表示的數為﹣1,點B表示的數為2.表示1的點C到點A的距離是2,到點B的距離是1,那么點C是(A,B)的妙點;又如,表示0的點D到點A的距離是1,到點B的距離是2,那么點D就不是(A,B)的妙點,但點D是(B,A)的妙點.
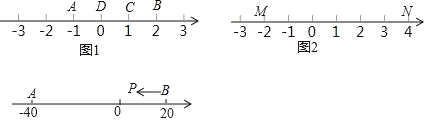
知識運用:如圖2,M、N為數軸上兩點,點M所表示的數為﹣2,點N所表示的數為4.
(1)數 所表示的點是(M,N)的妙點;
(2)如圖3,A、B為數軸上兩點,點A所表示的數為﹣40,點B所表示的數為20.現有一只電子螞蟻P從點B出發向左運動,到達點A停止.P點運動多少個單位時,P、A和B中恰有一個點為其余兩點的妙點?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】射擊隊為從甲、乙兩名運動員選拔一人參加運動會,對他們進行了六次測試,測試成績如下表(單位:環)
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 10 | 9 | 8 |
(1)由表格中的數據,計算出甲的平均成績是 環,乙的成績是 環.
(2)結合平均水平與發揮穩定性你認為推薦誰參加比賽更適合,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,四邊形ABCD和四邊形AECF都是矩形,AE與BC交于點M,CF與AD交于點N.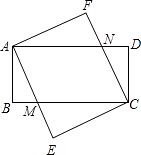
(1)求證:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF滿足何種關系時,四邊形AMCN是菱形,證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,D是BC邊上的一點,E是AD的中點,過A點作BC的平行線,交CE的延長線于點F,且AF=BD,連接BF.
(1)求證:BD=CD;(2)如果AB=AC,試判斷四邊形AFBD的形狀,并證明你的結論.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com