Question

【題目】如圖，已知∠ABC=90°，D是直線AB上的點，AD=BC．

（1）如圖1，過點A作AF⊥AB，截取AF=BD，連接DC、DF、CF，判斷△CDF的形狀并證明；

（2）如圖2，E是直線BC上一點，且CE=BD，直線AE、CD相交于點P，∠APD的度數是一個固定的值嗎？若是，請求出它的度數；若不是，請說明理由．

Answer 1

【答案】（1）△CDF是等腰三角形；（2）∠APD=45°．

【解析】試題分析：（1）利用SAS證明△AFD和△BDC全等，再利用全等三角形的性質得出FD=DC，即可判斷三角形的形狀；

（2）作AF⊥AB于A，使AF=BD，連結DF，CF，利用SAS證明△AFD和△BDC全等，再利用全等三角形的性質得出FD=DC，∠FDC=90°，即可得出∠FCD=∠APD=45°．

試題解析：（1）△CDF是等腰直角三角形，理由如下：

∵AF⊥AD，∠ABC=90°，∴∠FAD=∠DBC，

在△FAD與△DBC中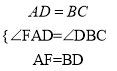， ，∴△FAD≌△DBC（SAS），

∴FD=DC，∴△CDF是等腰三角形，∵△FAD≌△DBC，∴∠FDA=∠DCB，

∵∠BDC+∠DCB=90°，∴∠BDC+∠FDA=90°，

∴△CDF是等腰直角三角形；

（2）作AF⊥AB于A，使AF=BD，連結DF，CF，如圖，∵AF⊥AD，∠ABC=90°，

∴∠FAD=∠DBC，在△FAD與△DBC中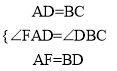， ，∴△FAD≌△DBC（SAS），

∴FD=DC，∴△CDF是等腰三角形，∵△FAD≌△DBC，∴∠FDA=∠DCB，

∵∠BDC+∠DCB=90°，∴∠BDC+∠FDA=90°，∴△CDF是等腰直角三角形，

∴∠FCD=45°，∵AF∥CE，且AF=CE，∴四邊形AFCE是平行四邊形，

∴AE∥CF，∴∠APD=∠FCD=45°．