
【題目】如圖所示,![]() 中,
中,![]() .現想利用三角形全等證明
.現想利用三角形全等證明![]() ,則圖中所添加的輔助線應是___________.
,則圖中所添加的輔助線應是___________.

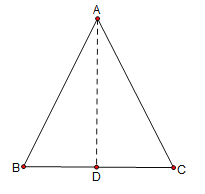
【答案】過點A作![]() ,垂足為D(或取BC的中點D或作∠A的角平分線交BC于點D),連接AD
,垂足為D(或取BC的中點D或作∠A的角平分線交BC于點D),連接AD
【解析】
要證明![]() ,則作輔助線時則須把
,則作輔助線時則須把![]() 和
和![]() 置于兩個全等三角形中,由此添加輔助線即可.
置于兩個全等三角形中,由此添加輔助線即可.
因為要證明![]() ,則須把
,則須把![]() 和
和![]() 置于兩個全等三角形中,
置于兩個全等三角形中,
所以添加輔助線時,將△ABC分成分別含![]() 、
、![]() 的兩個全等三角形,
的兩個全等三角形,
所以輔助線方法有:
①過點A作![]() ,垂足為D,連接AD,如圖所示,則△ABD和△ACD為直角三角形,根據AB=AC,AD=AD可證明△ABD≌△ACD(HL),從而得到
,垂足為D,連接AD,如圖所示,則△ABD和△ACD為直角三角形,根據AB=AC,AD=AD可證明△ABD≌△ACD(HL),從而得到![]() ;
;
②取BC的中點D,連接AD,如圖所示,則BD=CD,再根據AB=AC,AD=AD可證明△ABD≌△ACD(SSS),從而得到![]() ;
;
③作∠A的角平分線交BC于點D,如圖所示,則∠BAD=∠CAD,再根據根據AB=AC,AD=AD可證明△ABD≌△ACD(SAS),從而得到![]() .
.
故答案為:過點A作![]() ,垂足為D(或取BC的中點D或作∠A的角平分線交BC于點D),連接AD.
,垂足為D(或取BC的中點D或作∠A的角平分線交BC于點D),連接AD.


 能力評價系列答案
能力評價系列答案 唐印文化課時測評系列答案
唐印文化課時測評系列答案科目:初中數學 來源: 題型:
【題目】已知線段![]() 和線段
和線段![]() .
.

(1)按要求作圖(保留作圍痕跡,不寫作法);
延長線段![]() 至點
至點![]() ,使
,使![]() ,反向延長線段
,反向延長線段![]() 至點
至點![]() ,使
,使![]() ;
;
(2)如果![]() ,
,![]() 分別是線段
分別是線段![]() ,
,![]() 的中點,且
的中點,且![]() ,
,![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“綠水青山就是金山銀山”.為保護生態環境,A、B兩村準備各自清理所屬區域養魚網箱和捕魚網箱,每村參加清理人數及總開支如下表:

(1)若兩村清理同類漁具的人均支出費用一樣,求清理養魚網箱和捕魚網箱的人均支出費用各是多少元?
(2)在人均支出費用不變的情況下,為節約開支,兩村準備協調40人共同清理養魚網箱和捕魚網箱.要使總支出不超過102000元,且清理養魚網箱人數小于清理捕魚網箱人數,則有哪幾種分配清理人員方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點D,E分別在AC,AB上.

【1】(1) 已知,BD=CE,CD=BE,求證:AB=AC;
【2】(2) 分別將“BD=CE”記為①,“CD=BE” 記為②,“AB=AC”記為③.添加條件①、③,以②為結論構成命題1,添加條件②、③以①為結論構成命題2.命題1是命題2的 命題,命題2是
命題.(選擇“真”或“假”填入空格).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 經過
經過![]() 頂點
頂點![]() 的一條直線,
的一條直線,![]() .
.![]() 分別是直線
分別是直線![]() 上兩點,且
上兩點,且![]() .
.
(1)若直線![]() 經過
經過![]() 的內部,且
的內部,且![]() 在射線
在射線![]() 上,請解決下面兩個問題:
上,請解決下面兩個問題:
①如圖1,若![]() ,
,![]() ,
,
則![]()
![]() ;
;![]()
![]() (填“
(填“![]() ”,“
”,“![]() ”或“
”或“![]() ”);
”);
②如圖2,若![]() ,請添加一個關于
,請添加一個關于![]() 與
與![]() 關系的條件 ,使①中的兩個結論仍然成立,并證明兩個結論成立.
關系的條件 ,使①中的兩個結論仍然成立,并證明兩個結論成立.
(2)如圖3,若直線![]() 經過
經過![]() 的外部,
的外部,![]() ,請提出
,請提出![]() 三條線段數量關系的合理猜想(不要求證明).
三條線段數量關系的合理猜想(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
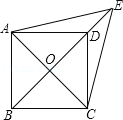
【題目】如圖,已知平行四邊形ABCD中,對角線AC,BD交于點O,E是BD延長線上的點,且△ACE是等邊三角形.
(1)求證:四邊形ABCD是菱形;
(2)若∠AED=2∠EAD,求證:四邊形ABCD是正方形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com