
【題目】如圖,在平面直角坐標系中,![]() ,P為x軸正半軸一動點,BC平分
,P為x軸正半軸一動點,BC平分![]() ,PC平分
,PC平分![]() ,OD平分
,OD平分![]()
![]() 求
求![]() 的度數;
的度數;
![]() 求證:
求證:![]() ;
;
![]() 在運動中,
在運動中,![]() 的值是否變化?若發生變化,說明理由;若不變,求其值.
的值是否變化?若發生變化,說明理由;若不變,求其值.

【答案】![]() 30°;
30°;![]() 證明見解析;
證明見解析;![]() 不變,105°.
不變,105°.
【解析】
(1)在Rt△AOB中根據已知和兩銳角互余的性質即可求出∠BAO的度數;
(2)根據外角的性質表示出∠C,得到∠C與∠OAP之間的數量關系;
(3)根據對頂角相等,分別表示出∠C和∠D,得到∠C+∠D的值.
![]() ∵∠ABO+∠BAO+∠AOB=180°,∠AOB=90°,∠ABO=2∠BAO,
∵∠ABO+∠BAO+∠AOB=180°,∠AOB=90°,∠ABO=2∠BAO,
∴2∠BAO+∠BAO+90°=180°,
∴∠BAO=30°;
![]() ∵∠CBP=
∵∠CBP=![]() ∠ABO,∠ABO=2∠BAO,∠BAO=30°,
∠ABO,∠ABO=2∠BAO,∠BAO=30°,
∴∠CBP=30°,
∵∠CPF=∠C+∠CBP,∠APF=∠OAP+∠AOP,∠CPF=![]() ∠APF,
∠APF,
∴∠C+∠CBP=![]() (∠OAP+∠AOP),
(∠OAP+∠AOP),
∵∠AOP=90°,
∴∠C+30°=![]() (∠OAP+90°)=
(∠OAP+90°)=![]() ∠OAP+45°,
∠OAP+45°,
∴∠C=15°+![]() ∠OAP;
∠OAP;
![]() 不變,
不變,
∵∠D+∠DOP+∠OPD=180°,∠DOP=![]() ∠EOF=
∠EOF=![]() ×90°=45°,
×90°=45°,
∴∠D+45°+∠OPD=180°,
∵∠OPD=∠C+∠CBP,
∴∠D+45°+∠C+∠CBP=180°,
∵∠CBP=30°,
∴∠D+∠C=180°-45°-∠CBP=135°-30°=105°,
∴∠D+∠C=105°,保持不變.


科目:初中數學 來源: 題型:
【題目】若直線l1經過點(0,4),l2經過(3,2),且l1與l2關于x軸對稱,則l1與l2的交點坐標為
A. (-2,0) B. (2,0) C. (-6,0) D. (6,0)
查看答案和解析>>
科目:初中數學 來源: 題型:
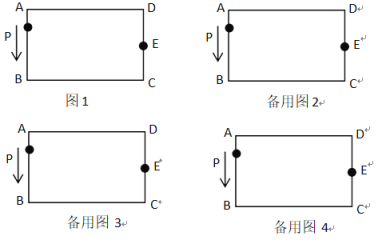
【題目】如圖,長方形ABCD,AB=CD=4,BC=AD=8,∠A=∠B=∠C=∠D=90°,E為CD邊的中點,P為長方形ABCD邊上的動點,動點P從A出發,沿著A B C E運動到E點停止,設點P經過的路程為![]() ,APE的面積為
,APE的面積為![]() .
.
(1)當![]() 時,在圖1中畫出草圖,并求出對應
時,在圖1中畫出草圖,并求出對應![]() 的值;
的值;
(2)利用備用圖畫出草圖,寫出![]() 與
與![]() 之間的關系式.
之間的關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列敘述不正確的是( )
A. 一個三角形必有三條中位線
B. 一個三角形必有三條中線
C. 三角形的一條中線分成的兩個三角形的面積相等
D. 三角形的一條中位線分成的兩部分面積相等
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把下列各數分別填入它所屬于的集合的括號內.
9,![]() ,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
,+4.3,|﹣0.5|,﹣(+7),18%,(﹣13)4,﹣6,0.
正分數集合{_________}
負分數集合{_________}
負整數集合{__________}
非負整數集合{________}.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c的頂點D(﹣1,2),與x軸的一個交點A在點(﹣3,0)和(﹣2,0)之間,其部分圖象如圖,則以下結論:①b2﹣4ac<0;②a+b+c>0;③c﹣a=2;④方程ax2+bx+c﹣2=0有兩個相等的實數根. 其中正確的結論是( )
A.③④
B.②④
C.②③
D.①④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)一天數學老師布置了一道數學題:已知x=2017,求整式![]() 的值,小明觀察后提出:“已知x=2017是多余的”,你認為小明的說法有道理嗎?請解釋.
的值,小明觀察后提出:“已知x=2017是多余的”,你認為小明的說法有道理嗎?請解釋.
(2)已知整式![]() ,整式M與整式N之差是
,整式M與整式N之差是![]() .
.
①求出整式N.
②若a是常數,且2M+N的值與x無關,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
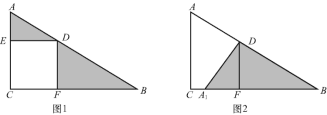
【題目】如圖,在Rt△ACB中,四邊形DECF為正方形,回答下列問題.
(1)簡述圖1經過怎樣的變換可形成圖2?
(2)若AD=3,BD=4,求△ADE與△BDF的面積之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com