
【題目】如圖,已知⊙O是△ABC的外接圓,AD是⊙O的直徑,且BD=BC,延長(zhǎng)AD到E,且有∠EBD=∠CAB.
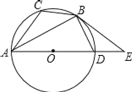
⑴求證:BE是⊙O的切線(xiàn);
⑵若BC=![]() ,AC=5,求圓的直徑AD的長(zhǎng).
,AC=5,求圓的直徑AD的長(zhǎng).
【答案】(1)詳見(jiàn)解析;(2)6
【解析】
(1)先根據(jù)等弦所對(duì)的劣弧相等,再結(jié)合∠EBD=∠CAB從而得到∠BAD=∠EBD,最后用直徑所對(duì)的圓周角為直角即可;
(2)利用三角形的中位線(xiàn)先求出OM,再用勾股定理求出半徑r,最后得到直徑的長(zhǎng).
解:⑴證明:連接OB,CD,OB、CD交于點(diǎn)M
∵BC=BD,

∴∠CAB=∠BAD.
∵OA=OB,
∴∠BAD=∠OBA.
∴∠CAB=∠OBA.
∴OB∥AC.
又AD是直徑,
∴∠ABD=∠ACD =90°,
又∠EBD=∠CAB, ∠CAB=∠OBA.
∴∠OBE=90°,即OB⊥BE.
又OB是半徑,
∴BE是⊙O的切線(xiàn).
⑵∵ OB∥AC, OA=OD,AC=5,.
∴ OM=2.5 ,BM=OB-2.5,OB⊥CD
設(shè)⊙O的半徑為r,則
在Rt△OMD中:MD2=r2-2.52;
在Rt△BMD中:MD2=BD2-(r-2.5)2 ,BD=BC=![]() .
.
∴r1=3 ,r2=-0.5(舍).
∴圓的直徑AD的長(zhǎng)是6.


 閱讀快車(chē)系列答案
閱讀快車(chē)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
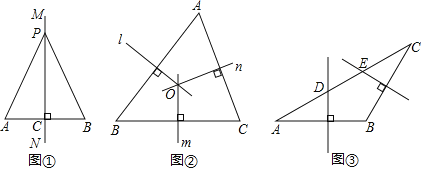
【題目】教材呈現(xiàn):下圖是華師版八年級(jí)上冊(cè)數(shù)學(xué)教材第94頁(yè)的部分內(nèi)容.
線(xiàn)段垂直平分線(xiàn)
我們已知知道線(xiàn)段是軸對(duì)稱(chēng)圖形,線(xiàn)段的垂直一部分線(xiàn)是線(xiàn)段的對(duì)稱(chēng)軸,如圖直線(xiàn)![]() 是線(xiàn)段
是線(xiàn)段![]() 的垂直平分線(xiàn),
的垂直平分線(xiàn),![]() 是
是![]() 上任一點(diǎn),連結(jié)
上任一點(diǎn),連結(jié)![]() 、
、![]() ,將線(xiàn)段
,將線(xiàn)段![]() 與直線(xiàn)
與直線(xiàn)![]() 對(duì)稱(chēng),我們發(fā)現(xiàn)
對(duì)稱(chēng),我們發(fā)現(xiàn)![]() 與
與![]() 完全重合,由此都有:線(xiàn)段垂直平分線(xiàn)的性質(zhì)定理,線(xiàn)段垂直平分線(xiàn)上的點(diǎn)到線(xiàn)段的距離相等.
完全重合,由此都有:線(xiàn)段垂直平分線(xiàn)的性質(zhì)定理,線(xiàn)段垂直平分線(xiàn)上的點(diǎn)到線(xiàn)段的距離相等.
已知:如圖,![]() ,垂足為點(diǎn)
,垂足為點(diǎn)![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 是直線(xiàn)
是直線(xiàn)![]() 上的任意一點(diǎn).
上的任意一點(diǎn).
求證:![]() .
.
圖中的兩個(gè)直角三角形![]() 和
和![]() ,只要證明這兩個(gè)三角形全等,便可證明
,只要證明這兩個(gè)三角形全等,便可證明![]() (請(qǐng)寫(xiě)出完整的證明過(guò)程)
(請(qǐng)寫(xiě)出完整的證明過(guò)程)
請(qǐng)根據(jù)教材中的分析,結(jié)合圖①,寫(xiě)出“線(xiàn)段垂直平分線(xiàn)的性質(zhì)定理”完整的證明過(guò)程,定理應(yīng)用.
(1)如圖②,在![]() 中,直線(xiàn)
中,直線(xiàn)![]() 、
、![]() 、
、![]() 分別是邊
分別是邊![]() 、
、![]() 、
、![]() 的垂直平分線(xiàn).
的垂直平分線(xiàn).
求證:直線(xiàn)![]() 、
、![]() 、
、![]() 交于點(diǎn).
交于點(diǎn).
(2)如圖③,在![]() 中,
中,![]() ,邊
,邊![]() 的垂直平分線(xiàn)交
的垂直平分線(xiàn)交![]() 于點(diǎn)
于點(diǎn)![]() ,邊
,邊![]() 的垂直平分線(xiàn)交
的垂直平分線(xiàn)交![]() 于點(diǎn)
于點(diǎn)![]() ,若
,若![]() ,
,![]() ,則
,則![]() 的長(zhǎng)為_(kāi)______.
的長(zhǎng)為_(kāi)______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】圖1是一種推磨工具模型,圖2是它的示意圖,已知AB⊥PQ,AP=AQ=3dm,AB=12dm,點(diǎn)A在中軸線(xiàn)l上運(yùn)動(dòng),點(diǎn)B在以O為圓心,OB長(zhǎng)為半徑的圓上運(yùn)動(dòng),且OB=4dm.
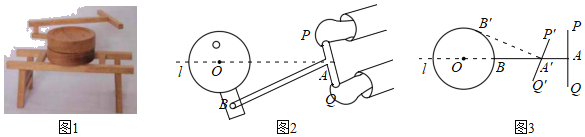
(1)如圖3,當(dāng)點(diǎn)B按逆時(shí)針?lè)较蜻\(yùn)動(dòng)到B′時(shí),A′B′與⊙O相切,則AA′=__dm.
(2)在點(diǎn)B的運(yùn)動(dòng)過(guò)程中,點(diǎn)P與點(diǎn)O之間的最短距離為__dm.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】拋物線(xiàn)![]() 經(jīng)過(guò)點(diǎn)(﹣2,0),且對(duì)稱(chēng)軸為直線(xiàn)x=1,其部分圖象如圖所示.對(duì)于此拋物線(xiàn)有如下四個(gè)結(jié)論:
經(jīng)過(guò)點(diǎn)(﹣2,0),且對(duì)稱(chēng)軸為直線(xiàn)x=1,其部分圖象如圖所示.對(duì)于此拋物線(xiàn)有如下四個(gè)結(jié)論:
①![]() ;
;
②![]() >
>![]() ;
;
③若n>m>0,則![]() 時(shí)的函數(shù)值小于
時(shí)的函數(shù)值小于![]() 時(shí)的函數(shù)值;
時(shí)的函數(shù)值;
④點(diǎn)(![]() ,0)一定在此拋物線(xiàn)上.
,0)一定在此拋物線(xiàn)上.
其中正確結(jié)論的個(gè)數(shù)是( )
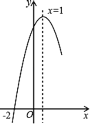
A.4個(gè)B.3個(gè)
C.2個(gè)D.1個(gè)
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線(xiàn)y=![]() 的圖像與
的圖像與![]() 軸的一個(gè)交點(diǎn)為A(-1,0),另一個(gè)交點(diǎn)為B,與
軸的一個(gè)交點(diǎn)為A(-1,0),另一個(gè)交點(diǎn)為B,與![]() 軸交于點(diǎn)C(0,﹣3),頂點(diǎn)為D.
軸交于點(diǎn)C(0,﹣3),頂點(diǎn)為D.
(1)求二次函數(shù)的解析式和點(diǎn)D的坐標(biāo);
(2)若點(diǎn)M是拋物線(xiàn)在![]() 軸下方圖像上的一動(dòng)點(diǎn),過(guò)點(diǎn)M作MN∥
軸下方圖像上的一動(dòng)點(diǎn),過(guò)點(diǎn)M作MN∥![]() 軸交線(xiàn)段BC于點(diǎn)N,當(dāng)MN取最大值時(shí),點(diǎn)M 的坐標(biāo);
軸交線(xiàn)段BC于點(diǎn)N,當(dāng)MN取最大值時(shí),點(diǎn)M 的坐標(biāo);
(3)將該拋物線(xiàn)向上或向下平移,使得新拋物線(xiàn)的頂點(diǎn)D落在x軸上,原拋物線(xiàn)上一點(diǎn)P平移后的對(duì)應(yīng)點(diǎn)為Q,如果∠OQP=∠OPQ,試求點(diǎn)Q的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
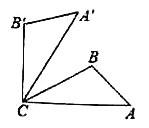
【題目】如圖,將![]() 繞點(diǎn)
繞點(diǎn)![]() 按逆時(shí)針?lè)较蛐D(zhuǎn)
按逆時(shí)針?lè)较蛐D(zhuǎn)![]() 后得到
后得到![]() ,若
,若![]() ,
,![]() ,且
,且![]() ,則
,則![]() ,
,![]() 兩點(diǎn)之間的距離為( )
兩點(diǎn)之間的距離為( )
A.![]() B.
B.![]()
C.2D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,拋物線(xiàn)經(jīng)過(guò)![]() ,
,![]() ,
,![]() 三點(diǎn).
三點(diǎn).
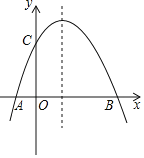
(1)求拋物線(xiàn)的解析式;
(2)在拋物線(xiàn)的對(duì)稱(chēng)軸上有一點(diǎn)![]() ,使
,使![]() 的值最小,求點(diǎn)
的值最小,求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(3)點(diǎn)![]() 為
為![]() 軸上一動(dòng)點(diǎn),在拋物線(xiàn)上是否存在一點(diǎn)
軸上一動(dòng)點(diǎn),在拋物線(xiàn)上是否存在一點(diǎn)![]() ,使以
,使以![]() ,
,![]() ,
,![]() ,
,![]() 四點(diǎn)構(gòu)成的四邊形為平行四邊形?若存在,求點(diǎn)
四點(diǎn)構(gòu)成的四邊形為平行四邊形?若存在,求點(diǎn)![]() 的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
的坐標(biāo);若不存在,請(qǐng)說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,某辦公樓AB的右邊有一建筑物CD,在建設(shè)物CD離地面2米高的點(diǎn)E處觀測(cè)辦公樓頂A點(diǎn),測(cè)得的仰角![]() =
=![]() ,在離建設(shè)物CD 25米遠(yuǎn)的F點(diǎn)觀測(cè)辦公樓頂A點(diǎn),測(cè)得的仰角
,在離建設(shè)物CD 25米遠(yuǎn)的F點(diǎn)觀測(cè)辦公樓頂A點(diǎn),測(cè)得的仰角![]() =
=![]() (B,F,C在一條直線(xiàn)上).
(B,F,C在一條直線(xiàn)上).
(1)求辦公樓AB的高度;
(2)若要在A,E之間掛一些彩旗,請(qǐng)你求出A,E之間的距離.(參考數(shù)據(jù):![]() )
)
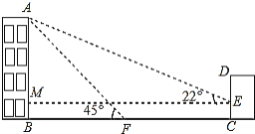
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】為提高學(xué)生身體素質(zhì),某校決定開(kāi)展足球、籃球、排球、兵乓球等四項(xiàng)課外體育活動(dòng),要求全員參與,并且每名學(xué)生只能選擇其中一項(xiàng).為了解選擇各種體育活動(dòng)項(xiàng)目的學(xué)生人數(shù),該校隨機(jī)抽取了部分學(xué)生進(jìn)行調(diào)查,并繪制出如下兩幅不完整的統(tǒng)計(jì)圖,請(qǐng)根據(jù)統(tǒng)計(jì)圖回答下列問(wèn)題:
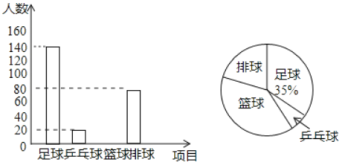
(1)直接寫(xiě)出這次抽樣調(diào)查的學(xué)生人數(shù);
(2)補(bǔ)全條形統(tǒng)計(jì)圖;
(3)若該學(xué)校總?cè)藬?shù)是1500人,請(qǐng)估計(jì)選擇籃球項(xiàng)目的學(xué)生約有多少人?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com