
【題目】為了解學生對博鰲論壇會的了解情況,某中學隨機抽取了部分學生進行問卷調查,將調查結果記作“![]() 非常了解,
非常了解,![]() 了解,
了解,![]() 了解較少,
了解較少,![]() 不了解.”四類分別統計,并繪制了下列兩幅統計圖(不完整).請根據圖中信息,解答下列問題:
不了解.”四類分別統計,并繪制了下列兩幅統計圖(不完整).請根據圖中信息,解答下列問題:
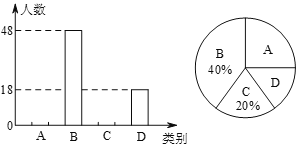
(1)此次共調查了______名學生;扇形統計圖中![]() 所在的扇形的圓心角度數為______;
所在的扇形的圓心角度數為______;
(2)將條形統計圖補充完整;
(3)若該校共有1600名學生,請你估計對博鰲論壇會的了解情況為“非常了解”的學生約有多少人?
【答案】(1)120;54°;(2)補圖見解析;(3) 400人.
【解析】
(1)由B類別人數及其所占百分比可得;用總人數乘以D類別人數占總人數的比例即可得;
(2)先用總人數乘以C類別的百分比求得其人數,再根據各類別百分比之和等于總人數求得A的人數即可補全圖形;
(3)用總人數乘以樣本中A類別的人數所占比例即可得.
(1)本次調查的總人數為48÷40%=120(名),
扇形統計圖中D所在的扇形的圓心角為360°×![]() =54°,
=54°,
故答案為120;54°;
(2)C類別人數為120×20%=24(人),
則A類別人數為120﹣(48+24+18)=30(人),
補全條形圖如下:
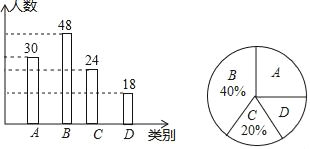
(3)估計對文明城市的了解情況為“非常了解”的學生的人數為1600×![]() =400(人).
=400(人).
答:該校對博鰲論壇會的了解情況為“非常了解”的學生約有400人.


科目:初中數學 來源: 題型:
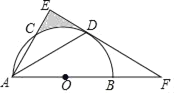
【題目】如圖,AB為半圓O的直徑,AC是⊙O的一條弦,D為![]() 的中點,作DE⊥AC,交AB的延長線于點F,連接DA.
的中點,作DE⊥AC,交AB的延長線于點F,連接DA.
(1)求證:EF為半圓O的切線;
(2)若DA=DF=6![]() ,求陰影區域的面積.(結果保留根號和π)
,求陰影區域的面積.(結果保留根號和π)
查看答案和解析>>
科目:初中數學 來源: 題型:
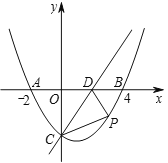
【題目】如圖,已知拋物線![]() 與x軸交于點A、B(點A位于點B左側),與y軸交于點C,CD∥x軸交拋物線于點D,M為拋物線的頂點.
與x軸交于點A、B(點A位于點B左側),與y軸交于點C,CD∥x軸交拋物線于點D,M為拋物線的頂點.
(1)求點A、B、C的坐標;
(2)設動點N(-2,n),求使MN+BN的值最小時n的值;
(3)P是拋物線上位于x軸上方的一點,請探究:是否存在點P,使以P、A、B為頂點的三角形與△ABD相似?若存在,求出點P的坐標;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形ABCD中,AB=8,點P在邊CD上,tan∠PBC=![]() ,點Q是在射線BP上的一個動點,過點Q作AB的平行線交射線AD于點M,點R在射線AD上,使RQ始終與直線BP垂直.
,點Q是在射線BP上的一個動點,過點Q作AB的平行線交射線AD于點M,點R在射線AD上,使RQ始終與直線BP垂直.
(1)如圖1,當點R與點D重合時,求PQ的長;
(2)如圖2,試探索: ![]() 的比值是否隨點Q的運動而發生變化?若有變化,請說明你的理由;若沒有變化,請求出它的比值;
的比值是否隨點Q的運動而發生變化?若有變化,請說明你的理由;若沒有變化,請求出它的比值;
(3)如圖3,若點Q在線段BP上,設PQ=x,RM=y,求y關于x的函數關系式,并寫出它的定義域.

查看答案和解析>>
科目:初中數學 來源: 題型:
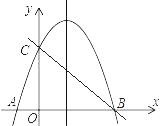
【題目】如圖,拋物線y=﹣x2+3x+4交x軸于A、B兩點(點A在B左邊),交y軸于點C.
(1)求A、B兩點的坐標;
(2)求直線BC的函數關系式;
(3)點P在拋物線的對稱軸上,連接PB,PC,若△PBC的面積為4,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,
,![]() ,與直線
,與直線![]() 交于點
交于點![]() ,直線
,直線![]() 與
與![]() 軸交于點
軸交于點![]() .
.
(1)求該拋物線的解析式.
(2)點![]() 是拋物線上第四象限上的一個動點,連接
是拋物線上第四象限上的一個動點,連接![]() ,
,![]() ,當
,當![]() 的面積最大時,求點
的面積最大時,求點![]() 的坐標.
的坐標.
(3)將拋物線的對稱軸向左平移3個長度單位得到直線![]() ,點
,點![]() 是直線
是直線![]() 上一點,連接
上一點,連接![]() ,
,![]() ,若直線
,若直線![]() 上存在使
上存在使![]() 最大的點
最大的點![]() ,請直接寫出滿足條件的點
,請直接寫出滿足條件的點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
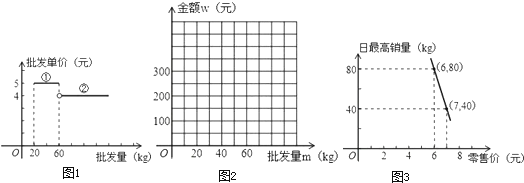
【題目】已知某種水果的批發單價與批發量的函數關系如圖1所示.
(1)請說明圖中①、②兩段函數圖象的實際意義;
(2)寫出批發該種水果的資金金額w(元)與批發量m(kg)之間的函數關系式;在圖2的坐標系中畫出該函數圖象;指出金額在什么范圍內,以同樣的資金可以批發到較多數量的該種水果;
(3)經調查,某經銷商銷售該種水果的日最高銷量與零售價之間的函數關系如圖3所示,該經銷商擬每日售出60kg以上該種水果,且當日零售價不變,請你幫助該經銷商設計進貨和銷售的方案,使得當日獲得的利潤最大.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC是等腰直角三角形,AB=AC,D為平面內的任意一點,且滿足CD=AC,若△ADB是以AD為腰的等腰三角形,則∠CDB的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
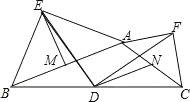
【題目】如圖,在鈍角三角形![]() 中,分別以
中,分別以![]() 和
和![]() 為斜邊向
為斜邊向![]() 的外側作等腰直角三角形
的外側作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,
,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,取
,取![]() 的中點
的中點![]() ,
,![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確結論有( )
.其中正確結論有( )
A. ![]() 個B.
個B. ![]() 個C.
個C. ![]() 個D.
個D. ![]() 個
個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com