
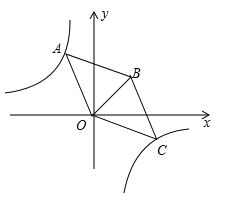
【題目】如圖,在平面直角坐標系中,菱形![]() 的頂點
的頂點![]() 為坐標原點,且與反比例函數(shù)
為坐標原點,且與反比例函數(shù)![]() 的圖象相交于
的圖象相交于![]() ,
,![]() 兩點,且
兩點,且![]() 點的縱坐標為
點的縱坐標為![]() ,已知點
,已知點![]() ,則
,則![]() 的值為( ).
的值為( ).
A.![]() B.
B.![]() C.9D.
C.9D.![]()
【答案】D
【解析】
作AE⊥x軸交x軸于點E,作CF⊥x軸交x軸于點F,作BD∥x軸交AE于點D,證明△ADB≌△CFO,求出AD=CF=![]() ,同理證明△AEO≌△OFC,求出OF=AE=
,同理證明△AEO≌△OFC,求出OF=AE=![]() ,得到點C坐標即可解決問題.
,得到點C坐標即可解決問題.
解:作AE⊥x軸交x軸于點E,作CF⊥x軸交x軸于點F,作BD∥x軸交AE于點D,

∵四邊形AOCB是菱形,
∴AB∥CO,AB=CO,
∴∠ABO=∠COB,
又∵BD∥x軸,
∴∠DBO=∠FOB,
∴∠ABD=∠COF,
∵AD⊥BD,CF⊥OF,
∴∠ADB=∠CFO=90°,
又∵AB=CO,
∴△ADB≌△CFO(AAS),
∴AD=CF,
∵C點的縱坐標為![]() ,
,![]() ,
,
∴AD=CF=![]() ,
,
∴AE=![]() ,
,
同理可證,△AEO≌△OFC,
∴OF=AE=![]() ,
,
∴點C的坐標為(![]() ,
,![]() ),
),
∴k=![]() ,
,
故選:D.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列說法正確的是( )
A.了解一批燈泡的使用壽命采用全面調(diào)查
B.一組數(shù)據(jù)6,5,3,5,4的眾數(shù)是5,中位數(shù)是3
C.“367人中必有2人的生日是同一天”是必然事件
D.一組數(shù)據(jù)10,11,12,9,8的平均數(shù)是10,方差是1.5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知二次函數(shù)![]() (
(![]() )的圖象與x軸交于點A(﹣1,0),對稱軸為直線x=1,與y軸的交點B在(0,2)和(0,3)之間(包括這兩點),下列結(jié)論:
)的圖象與x軸交于點A(﹣1,0),對稱軸為直線x=1,與y軸的交點B在(0,2)和(0,3)之間(包括這兩點),下列結(jié)論:
①當(dāng)x>3時,y<0;
②3a+b<0;
③![]() ;
;
④![]() ;
;
其中正確的結(jié)論是( )

A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
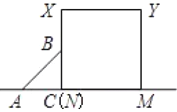
【題目】已知,如圖等腰直角![]() 沿MN所在的直線以
沿MN所在的直線以![]() 的速度向右作勻速直線運動,若
的速度向右作勻速直線運動,若![]() ,則
,則![]() 和正方形
和正方形![]() 重疊部分的面積
重疊部分的面積![]() 與勻速運動所有的時間
與勻速運動所有的時間![]() 之間函數(shù)的大致圖像是( )
之間函數(shù)的大致圖像是( )
A.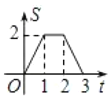 B.
B.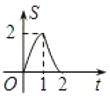 C.
C.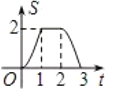 D.
D.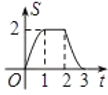
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知在四邊形ABCD中∠A=∠ABC=90°,點E是CD的中點,△ABD與 △EBD關(guān)于直線BD對稱,![]() ,
,![]() .
.
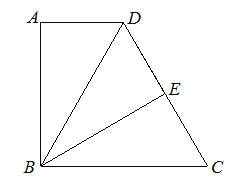
(1)求點A和點E之間的距離;
(2)聯(lián)結(jié)AC交BE于點F,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有這樣一個問題:探究函數(shù)![]() 的圖象與性質(zhì),小李根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗,對函數(shù)
的圖象與性質(zhì),小李根據(jù)學(xué)習(xí)函數(shù)的經(jīng)驗,對函數(shù)![]() 的圖象與性質(zhì)進行了探究.
的圖象與性質(zhì)進行了探究.
下面是小李探究的過程,請補充完整:
(1)函數(shù)![]() 的自變量
的自變量![]() 的取值范圍是______;
的取值范圍是______;
(2)下表是![]() 與
與![]() 的幾組對應(yīng)值:
的幾組對應(yīng)值:
| … |
|
|
| 0 | 2 | 3 | 4 | 5 | … |
| … | 0 |
|
|
| 5 | 3 |
| 2 | … |
則![]() 的值為_______;
的值為_______;
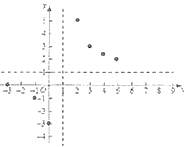
(3)如圖所示,在平面直角坐標系![]() 中,根據(jù)描出的點,請補全此函數(shù)的圖象;
中,根據(jù)描出的點,請補全此函數(shù)的圖象;
(4)觀察圖象,寫出該函數(shù)的一條性質(zhì)_______;
(5)若函數(shù)![]() 的圖象在函數(shù)
的圖象在函數(shù)![]() 的圖象上方,直接寫出
的圖象上方,直接寫出![]() 的取值范圍_______.
的取值范圍_______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
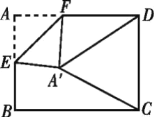
【題目】如圖,在矩形紙片![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是
是![]() 的中點,點
的中點,點![]() 是
是![]() 邊上的一個動點,將
邊上的一個動點,將![]() 沿
沿![]() 所在直線翻折,得到
所在直線翻折,得到![]() ,連接
,連接![]() ,
,![]() ,則當(dāng)
,則當(dāng)![]() 是以
是以![]() 為腰的等腰三角形時,
為腰的等腰三角形時,![]() 的長是___________.
的長是___________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知A(3,m),B(﹣2,﹣3)是直線AB和某反比例函數(shù)的圖象的兩個交點.
(1)求直線AB和反比例函數(shù)的解析式;
(2)觀察圖象,直接寫出當(dāng)x滿足什么范圍時,直線AB在雙曲線的下方;
(3)反比例函數(shù)的圖象上是否存在點C,使得△OBC的面積等于△OAB的面積?如果不存在,說明理由;如果存在,求出滿足條件的所有點C的坐標.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
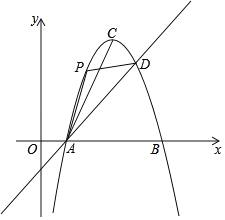
【題目】如圖,直線y=x﹣1與拋物線y=﹣x2+6x﹣5相交于A、D兩點.拋物線的頂點為C,連結(jié)AC.
(1)求A,D兩點的坐標;
(2)點P為該拋物線上一動點(與點A、D不重合),連接PA、PD.
①當(dāng)點P的橫坐標為2時,求△PAD的面積;
②當(dāng)∠PDA=∠CAD時,直接寫出點P的坐標.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com