
【題目】已知函數y=3x2﹣6x+k(k為常數)的圖像經過點A(0.8,y1),B(1.1,y2),C( ![]() ,y3),則有( )
,y3),則有( )
A.y1<y2<y3
B.y1>y2>y3
C.y3>y1>y2
D.y1>y3>y2
【答案】C
【解析】解:∵函數y=3x2﹣6x+k(k為常數),
∴對稱軸為x=1,圖像開口向上;
∴A(0.8,y1)在對稱軸的左側,根據二次函數圖像的對稱性可知,對稱點為(1.2,y1),在y軸的右邊y隨x的增大而增大,
因為1.1<1.2< ![]() ,于是y2<y1<y3
,于是y2<y1<y3
故選:C.
【考點精析】本題主要考查了二次函數的圖象和二次函數的性質的相關知識點,需要掌握二次函數圖像關鍵點:1、開口方向2、對稱軸 3、頂點 4、與x軸交點 5、與y軸交點;增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能正確解答此題.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:初中數學 來源: 題型:
【題目】已知等邊△ABC中,點D為射線BA上一點,作DE=DC,交直線BC于點E,∠ABC的平分線BF交CD于點F,過點A作AH⊥CD于H,當EDC=30![]() ,CF=
,CF=![]() ,則DH=______.
,則DH=______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形ABCD中,CD=6cm,當邊CD向右平移時,長方形的面積發生了變化.
(1)這個變化過程中,自變量、因變量各是什么?
(2)如果BC的長為![]() cm,那么長方形的面積
cm,那么長方形的面積![]() 可以表為 .
可以表為 .
(3)當BC的長從12cm增加到20cm時,長方形的面積增加了多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如圖①,求證:DE∥BC;
(2)若將圖①改變為圖②,其他條件不變,(1)中的結論是否仍成立?請說明理由.
如圖,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如圖①,求證:DE∥BC;
(2)若將圖①改變為圖②,其他條件不變,(1)中的結論是否仍成立?請說明理由.


查看答案和解析>>
科目:初中數學 來源: 題型:
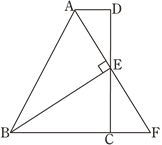
【題目】如圖,在四邊形ABCD中,AD∥BC,E為CD的中點,連接AE、BE,BE⊥AE,延長AE交BC的延長線于點F. 已知AD=2cm,BC=5cm.
(1)求證:FC=AD;
(2)求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數 ![]() 的圖像如圖所示,點A0位于坐標原點,點A1 , A2 , A3 , …,A2008在y軸的正半軸上,點B1 , B2 , B3 , …,B2008在二次函數
的圖像如圖所示,點A0位于坐標原點,點A1 , A2 , A3 , …,A2008在y軸的正半軸上,點B1 , B2 , B3 , …,B2008在二次函數 ![]() 位于第一象限的圖像上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都為等邊三角形,則△A2007B2008A2008的邊長=
位于第一象限的圖像上,若△A0B1A1 , △A1B2A2 , △A2B3A3 , …,△A2007B2008A2008都為等邊三角形,則△A2007B2008A2008的邊長=
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請把下面證明過程補充完整:
已知:如圖,∠ADC=∠ABC,BE、DF分別平分∠ABC、∠ADC,且∠1=∠2.
求證:∠A=∠C.

證明:∵BE、DF分別平分∠ABC、∠ADC(已知),
∴∠1=![]() ∠ABC,∠3=
∠ABC,∠3=![]() ∠ADC(角平分線定義).
∠ADC(角平分線定義).
∵∠ABC=∠ADC(已知),
∴∠1=∠3(等量代換),
∵∠1=∠2(已知),
∴∠2=∠3(等量代換).
∴_____∥_____ (___ __).
∴∠A+∠_____=180°,∠C+∠_____=180°(___ __).
∴∠A=∠C(___ __).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】畫圖并填空:如圖,每個小正方形的邊長為1個單位,每個小正方形的頂點叫格點.

(1)將△ABC向左平移8格,再向下平移1格.請在圖中畫出平移后的△A′B′C′
(2)利用網格在圖中畫出△ABC的中線CD,高線AE;
(3)△A′B′C′的面積為_____.
(4)在平移過程中線段BC所掃過的面積為 .
(5)在右圖中能使![]() 的格點P的個數有 個(點P異于A).
的格點P的個數有 個(點P異于A).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com