
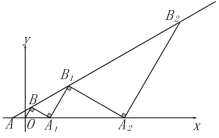
【題目】在直角坐標(biāo)系中,如圖所示,把∠BAO放在直角坐標(biāo)系中,使射線AO與x軸重合,已知BAO=30°,OA=OB=1,過(guò)點(diǎn)B作BA1⊥OB交x軸于A1,過(guò)點(diǎn)A1做B1A1⊥BA1交直線AB于點(diǎn)B1,過(guò)B1作B1A2⊥B1A1交x軸于點(diǎn)A2,再過(guò)A2依次作垂直….則△A6B6A7的面積為_____.
【答案】![]() .
.
【解析】
根據(jù)OA的長(zhǎng)即可求出A的坐標(biāo),根據(jù)OB和∠BOA1=60°,即可求出B的坐標(biāo),設(shè)直線AB的解析式是y=kx+b,把A、B的坐標(biāo)代入得出方程組,求出方程組的解;推出∠BAC=∠ABO=30°,求出∠BOC=60°,∠BA1O=30°,求出BA1=![]() ,求出A1B1=
,求出A1B1=![]() ×
×![]() 、B1A2=3
、B1A2=3![]() =
=![]() ×
×![]() ×
×![]() ,同理求出A6B6=12個(gè)
,同理求出A6B6=12個(gè)![]() 相乘,B6A7=13個(gè)
相乘,B6A7=13個(gè)![]() 相乘,根據(jù)三角形的面積公式求出即可.
相乘,根據(jù)三角形的面積公式求出即可.
∵OA=1,
∴A(-1,0),
易求B(![]() ,
,![]() ).
).
設(shè)直線AB的解析式是:y=kx+b,
把A(-1,0),B(![]() ,
,![]() )代入得:
)代入得:
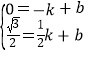 ,
,
解得: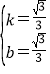 ,
,
∴直線AB的解析式為:y=![]() x+
x+![]() .
.
∵OB=OA=1,
∴∠BAC=∠ABO=30°,
∴∠BOC=60°,
∴∠BA1O=30°,
∴BA1=![]() ,
,
同理∠BB1A1=30°,
∴B1A1=3=![]() ×
×![]() ,
,
同理:B1A2=3![]() =
=![]() ×
×![]() ×
×![]() ,
,
…
A6B6=![]() ×
×![]() ×…×
×…×![]() (12個(gè)
(12個(gè)![]() 相乘),
相乘),
B6A7=![]() ×
×![]() ×…×
×…×![]() (13個(gè)
(13個(gè)![]() 相乘),
相乘),
∴△A6B6A7的面積是:![]() A6B6×B6A7=
A6B6×B6A7=![]() ×(
×(![]() ×
×![]() ×…×
×…×![]() )×(
)×(![]() ×
×![]() ×…×
×…×![]() )
)
=![]() ,
,
答:△A6B6A7的面積是![]() .
.


 王后雄學(xué)案教材完全解讀系列答案
王后雄學(xué)案教材完全解讀系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知![]() ,點(diǎn)
,點(diǎn)![]() 為平面內(nèi)一點(diǎn).
為平面內(nèi)一點(diǎn).
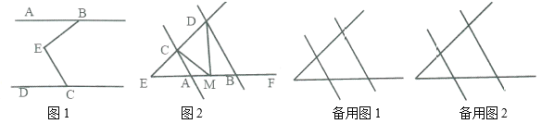
(1)如圖1,![]() 和
和![]() 互余,小明說(shuō)過(guò)
互余,小明說(shuō)過(guò)![]() 作
作![]() ,很容易說(shuō)明
,很容易說(shuō)明![]() 。請(qǐng)幫小明寫(xiě)出具體過(guò)程;
。請(qǐng)幫小明寫(xiě)出具體過(guò)程;
(2)如圖2,![]() ,當(dāng)點(diǎn)
,當(dāng)點(diǎn)![]() 在線段
在線段![]() 上移動(dòng)時(shí)(點(diǎn)
上移動(dòng)時(shí)(點(diǎn)![]() 與
與![]() ,
,![]() 兩點(diǎn)不重合),指出
兩點(diǎn)不重合),指出![]() 與
與![]() ,
,![]() 的數(shù)量關(guān)系?請(qǐng)說(shuō)明理由;
的數(shù)量關(guān)系?請(qǐng)說(shuō)明理由;
(3)在(2)的條件下,若點(diǎn)![]() 在
在![]() ,
,![]() 兩點(diǎn)外側(cè)運(yùn)動(dòng)(點(diǎn)
兩點(diǎn)外側(cè)運(yùn)動(dòng)(點(diǎn)![]() 與
與![]() ,
,![]() ,
,![]() 三點(diǎn)不重合)請(qǐng)直接寫(xiě)出
三點(diǎn)不重合)請(qǐng)直接寫(xiě)出![]() 與
與![]() ,
,![]() 的數(shù)量關(guān)系.
的數(shù)量關(guān)系.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】“瀏陽(yáng)河彎過(guò)九道彎,五十里水路到湘江.”如圖所示,某段河水流經(jīng) B,C,D 三點(diǎn)拐彎后與原來(lái)流向相同,若∠ABC =6∠CDE,∠BCD =4∠CDE,則∠CDE= _________.
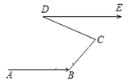
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平行四邊形ABCD的紙片中,AC⊥AB,AC與BD交于O,將△ABC沿對(duì)角線AC翻折得到![]() .
.
(1)求證:四邊形ACDB’是矩形.
(2)若平行四邊形ABCD的面積為12,求翻折后紙片重疊部分的面積,即![]() .
.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,點(diǎn)A,B的坐標(biāo)分別為A(1,0)、B(3,0).拋物線y=x2﹣2mx+m2﹣4的頂點(diǎn)為P,與y軸的交點(diǎn)為Q.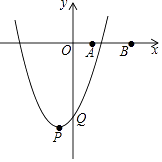
(1)填空:點(diǎn)P的坐標(biāo)為;點(diǎn)Q的坐標(biāo)為(均用含m的代數(shù)式表示)
(2)當(dāng)拋物線經(jīng)過(guò)點(diǎn)A時(shí),求點(diǎn)Q的坐標(biāo).
(3)連接QA、QB,設(shè)△QAB的面積為S,當(dāng)拋物線與線段AB有公共點(diǎn)時(shí),求S與m之間的函數(shù)關(guān)系式.
(4)點(diǎn)P、Q不重合時(shí),以PQ為邊作正方形PQMN(P、Q、M、N分別按順時(shí)針?lè)较蚺帕校?dāng)正方形PQMN的四個(gè)頂點(diǎn)中,位于x軸兩側(cè)或y軸兩側(cè)的頂點(diǎn)個(gè)數(shù)相同時(shí),直接寫(xiě)出此時(shí)m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在△ABC中,∠ABC=45°,∠ACB=60°,BC=2![]() +2,D是BC邊上異于點(diǎn)B,C的一動(dòng)點(diǎn),將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
+2,D是BC邊上異于點(diǎn)B,C的一動(dòng)點(diǎn),將三角形ABD沿AB翻折得到△ABD1,將△ACD沿AC翻折得到△ACD2,連接D1D2,則四邊形D1BCD2的面積的最大值是_____.
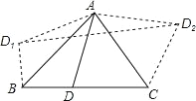
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】相傳,大禹治水時(shí),洛水中出現(xiàn)了一個(gè)“神龜”背上有美妙的圖案,史稱(chēng)“洛書(shū)”,用現(xiàn)在的數(shù)字翻譯出來(lái),就是三階幻方.三階幻方是最簡(jiǎn)單的幻方,又叫九宮格,它是由九個(gè)數(shù)字組成的一個(gè)三行三列的矩陣.其對(duì)角線、橫行、縱向的數(shù)字之和均相等,這個(gè)和叫做幻和,正中間那個(gè)數(shù)叫中心數(shù),如圖(1)是由![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 所組成的一個(gè)三階幻方,其幻和為
所組成的一個(gè)三階幻方,其幻和為![]() ,中心數(shù)為
,中心數(shù)為![]() .如圖(2)是一個(gè)新三階幻方,該新三階幻方的幻和為
.如圖(2)是一個(gè)新三階幻方,該新三階幻方的幻和為![]() 的
的![]() 倍,且
倍,且![]() ,則
,則![]() _______.
_______.


查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】小穎為媽媽準(zhǔn)備了一份生日禮物,禮物外包裝盒為長(zhǎng)方體形狀,長(zhǎng)、寬、高分別為![]() 、
、![]() 、
、![]()
![]() ,為了美觀,小穎決定在包裝盒外用絲帶打包裝飾,她發(fā)現(xiàn),可以用如圖所示的三種打包方式,所需絲帶的長(zhǎng)度分別為
,為了美觀,小穎決定在包裝盒外用絲帶打包裝飾,她發(fā)現(xiàn),可以用如圖所示的三種打包方式,所需絲帶的長(zhǎng)度分別為![]() ,
,![]() ,
,![]() (不計(jì)打結(jié)處絲帶長(zhǎng)度)
(不計(jì)打結(jié)處絲帶長(zhǎng)度)

(1)用含![]() 、
、![]() 、
、![]() 的代數(shù)式分別表示
的代數(shù)式分別表示![]() ,
,![]() ,
,![]() ;
;
(2)方法簡(jiǎn)介:
要比較兩數(shù)![]() 與
與![]() 大小,我們可以將
大小,我們可以將![]() 與
與![]() 作差,結(jié)果可能出現(xiàn)三種情況:
作差,結(jié)果可能出現(xiàn)三種情況:
①![]() ,則
,則![]() ;
;
②![]() ,則
,則![]() ;
;
③![]() ,則
,則![]() ;
;
我們將這種比較大小的方法叫做“作差法”.
請(qǐng)幫小穎選出最節(jié)省絲帶的打包方式,并說(shuō)明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】初中生在數(shù)學(xué)運(yùn)算中使用計(jì)算器的現(xiàn)象越來(lái)越普遍,某校一興趣小組隨機(jī)抽查了本校若干名學(xué)生使用計(jì)算器的情況.以下是根據(jù)抽查結(jié)果繪制出的不完整的條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖: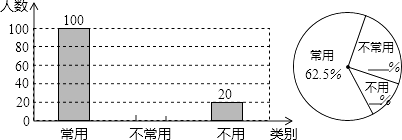
請(qǐng)根據(jù)上述統(tǒng)計(jì)圖提供的信息,完成下列問(wèn)題:
(1)這次抽查的樣本容量是;
(2)請(qǐng)補(bǔ)全上述條形統(tǒng)計(jì)圖和扇形統(tǒng)計(jì)圖;
(3)若從這次接受調(diào)查的學(xué)生中,隨機(jī)抽查一名學(xué)生恰好是“不常用”計(jì)算器的概率是多少?
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com