
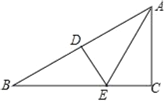
【題目】如圖,在△ABC中,∠B=30°,邊AB的垂直平分線分別交AB和BC于點D,E,且AE平分∠BAC.
(1)求∠C的度數;
(2)若CE=1,求AB的長.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)先由線段垂直平分線的性質及∠B=30°求出∠BAE=30°,再由AE平分∠BAC可得出∠EAC=∠BAE=30°,由三角形內角和定理即可求出∠C的度數.
(2)先求出∠EAC=30°,在Rt△AEC中,利用特殊角的三角函數求解直角三角形,可解得AC的長為![]() ,再在Rt△ABC中,利用特殊角的三角函數求解直角三角形,可解得AB 的長.
,再在Rt△ABC中,利用特殊角的三角函數求解直角三角形,可解得AB 的長.
(1)∵DE是線段AB的垂直平分線,∠B=30°,
∴∠BAE=∠B=30°,
∵AE平分∠BAC,
∴∠EAC=∠BAE=30°,
即∠BAC=60°,
∴∠C=180°﹣∠BAC﹣∠B=180°﹣60°﹣30°=90°.
(2)∵∠C=90°,∠B=30°,
∴∠BAC=60°
∵AE平分∠BAC
∴∠EAC=30°
∵CE=1,∠C=90°
∴AC=![]() =
=![]() ,
,
∴AB=![]() =2
=2![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,七巧板由圖中標號為“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”、“
”、“![]() ”的七塊板組成,七巧板是我們祖先的一項卓越創造,被稱為“東方魔板”,它雖然僅有七塊板組成,但用它們可以拼出各種各樣的圖形.請你按下列要求畫出所拼的圖,圖中往上標號:
”的七塊板組成,七巧板是我們祖先的一項卓越創造,被稱為“東方魔板”,它雖然僅有七塊板組成,但用它們可以拼出各種各樣的圖形.請你按下列要求畫出所拼的圖,圖中往上標號:

①用其中的四塊板拼成一個三角形;
②用其中的五塊板拼成一個正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在數軸上點A表示數a,點C表示數c,且![]() .我們把數軸上兩點之間的距離用表示兩點的大寫字母一起標記.
.我們把數軸上兩點之間的距離用表示兩點的大寫字母一起標記.
![]()
比如,點A與點B之間的距離記作AB.
(1)求AC的值;
(2)若數軸上有一動點D滿足CD+AD=36,直接寫出D點表示的數;
(3)動點B從數1對應的點開始向右運動,速度為每秒1個單位長度,同時點A,C在數軸上運動,點A、C的速度分別為每秒 3個單位長度,每秒4個單位長度,運動時間為t秒.
①若點A向右運動,點C向左運動,AB=BC,求t的值.
②若點A向左運動,點C向右運動,2AB-m×BC的值不隨時間t的變化而改變,請求出m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:a是單項式-xy2的系數,b是最小的正整數,c是多項式2m2n-m3n2-m-2的次數.請回答下列問題:
(1)請直接寫出a、b、c的值.a= ,b= ,c= .
(2)數軸上,a、b、c三個數所對應的點分別為A、B、C,點A、B、C同時開始在數軸上運動,若點A以每秒1個單位長度的速度向左運動,同時,點B和點C分別以每秒1個單位長度和3個單位長度的速度向右運動,假設t秒鐘過后,若點B與點c之間的距離表示為BC,點A與點C之間的距離表示為AC,點A與點C之間的距離表示為AC.
①t秒鐘過后,AC的長度為 (用含t的關系式表示);
②請問:BC-AB的值是否會隨著時間t的變化而改變?若變化,請說明理由;若不變,請求出其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在網絡時代里,每年網絡上都會出現很多紅極一時的網絡流行語,為了解同學們對網絡流行語的使用情況,某數學興趣小組選取了其中的 A:“藍瘦香菇”,B:“洪荒之力”,C:“老司機”,D:“套路”四個網絡流行語在全校3000名學生中進行了抽樣調查,要求每位被調查學生只能從中選擇一個自己用得最多的網絡流行語.根據調查結果,該小組繪制了如下兩幅不完整的統計圖,根據圖中提供的信息,請補全條形統計圖并估計該校學生用得最多的網絡流行語.
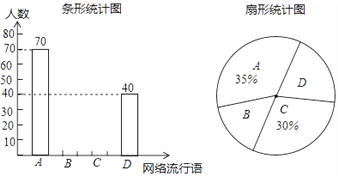
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)5![]() -3
-3![]() +4
+4![]() -
-![]()
(2)(![]() -
-![]() -
-![]() )×(-36)
)×(-36)
(3)-![]() ―(1―0.5)÷
―(1―0.5)÷![]() ×[2+(-4)2]
×[2+(-4)2]
(4)(![]() -
-![]() )×52÷|-
)×52÷|-![]() |+(
|+(![]() )2019×42020
)2019×42020
查看答案和解析>>
科目:初中數學 來源: 題型:
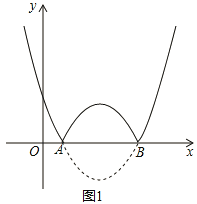
【題目】如圖,拋物線![]() :
:![]() 與x軸交于A,B兩點(點A在點B的左側),將拋物線l在x軸下方部分沿x軸翻折,x軸上方的圖像保持不變,就組成了函數
與x軸交于A,B兩點(點A在點B的左側),將拋物線l在x軸下方部分沿x軸翻折,x軸上方的圖像保持不變,就組成了函數![]() 的圖像.
的圖像.
(1)若點A的坐標為(1,0).
①求拋物線![]() 的表達式,并直接寫出當x為何值時,函數
的表達式,并直接寫出當x為何值時,函數![]() 的值y隨x的增大而增大;
的值y隨x的增大而增大;
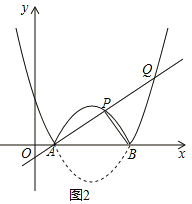
②如圖2,若過A點的直線交函數![]() 的圖像于另外兩點P,Q,且
的圖像于另外兩點P,Q,且![]() ,求點P的坐標;
,求點P的坐標;
(2)當![]() 時,若函數
時,若函數![]() 的值y隨x的增大而增大,直接寫出h的取值范圍.
的值y隨x的增大而增大,直接寫出h的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在學習了有理數的加減法之后,老師講解了例題![]() 的計算思路為:將兩個加數組合在一起作為一組,其和為1,共有1010組,所以結果為+1010.
的計算思路為:將兩個加數組合在一起作為一組,其和為1,共有1010組,所以結果為+1010.
根據這個思路學生改編了下列幾題:
(1)計算:①![]()
②![]()
(2)螞蟻在數軸的原點![]() 處,第一次向右爬行1個單位,第二次向右爬行2個單位,第三次向左爬行3個單位,第四次向左爬行4個單位,第五次向右爬行5個單位,第六次向右爬行6個單位,第七次向左爬行7個單位……
處,第一次向右爬行1個單位,第二次向右爬行2個單位,第三次向左爬行3個單位,第四次向左爬行4個單位,第五次向右爬行5個單位,第六次向右爬行6個單位,第七次向左爬行7個單位……
①按照這個規律,第1024次爬行后螞蟻所在位置在原點左側還是右側?對應哪個數?
②按照這個規律,第 次爬行后螞蟻在數軸上表示751的位置.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料,解答相應的問題:
如果一個正整數能表示為兩個正整數的平方差,那么稱這個正整數為“智慧數”,否則,稱這個正整數為“非慧數”。
例如:![]() …
…
因此:3,5,8,……都是“智慧數”;而1,2,4……都是“非智慧數”。
對于“智慧數”,有如下結論:
①設![]() 為正整數(
為正整數(![]() ),則
),則![]() ,∴除1以外,所有的奇數都是“智慧數”;
,∴除1以外,所有的奇數都是“智慧數”;
②設![]() 為正整數(
為正整數(![]() ),則
),則![]() = ,∴
= ,∴
都是“智慧數”;
(1)補全材料中空缺的部分;
(2)求出所有大于5而小于20的“非智慧數”;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com