
【題目】如圖,在平行四邊形ABCD中,![]() ,
,![]() 的平分線與BC的延長線交于點E,與DC交于點F,且點F為邊DC的中點,
的平分線與BC的延長線交于點E,與DC交于點F,且點F為邊DC的中點,![]() ,垂足為G,若
,垂足為G,若![]() ,則AE的邊長為
,則AE的邊長為![]()
![]()

A. ![]() B.
B. ![]() C. 4 D. 8
C. 4 D. 8
【答案】B
【解析】
試題由AE為角平分線,得到一對角相等,再由ABCD為平行四邊形,得到AD與BE平行,利用兩直線平行內錯角相等得到一對角相等,等量代換及等角對等邊得到AD=DF,由F為DC中點,AB=CD,求出AD與DF的長,得出三角形ADF為等腰三角形,根據三線合一得到G為AF中點,在直角三角形ADG中,由AD與DG的長,利用勾股定理求出AG的長,進而求出AF的長,再由三角形ADF與三角形ECF全等,得出AF=EF,即可求出AE的長.∵AE為∠DAB的平分線,∴∠DAE=∠BAE,∵DC∥AB,∴∠BAE=∠DFA,∴∠DAE=∠DFA,∴AD=FD,又F為DC的中點,∴DF=CF,∴AD=DF=![]() DC=
DC=![]() AB=2,在Rt△ADG中,根據勾股定理得:AG=
AB=2,在Rt△ADG中,根據勾股定理得:AG=![]() ,則AF=2AG=2
,則AF=2AG=2![]() ,∵平行四邊形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,
,∵平行四邊形ABCD,∴AD∥BC,∴∠DAF=∠E,∠ADF=∠ECF,在△ADF和△ECF中,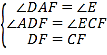 ,∴△ADF≌△ECF(AAS),∴AF=EF,則AE=2AF=4
,∴△ADF≌△ECF(AAS),∴AF=EF,則AE=2AF=4![]() .故選:B.
.故選:B.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】A、B兩地果園分別有橘子40噸和60噸,C、D兩地分別需要橘子30噸和70噸;已知從A、B到C、D的運價如表:
到C地 | 到D地 | |
A果園 | 每噸15元 | 每噸12元 |
B果園 | 每噸10元 | 每噸9元 |
(1)若從A果園運到C地的橘子為x噸,則從A果園運到D地的橘子為 ____噸,
從A果園將橘子運往D地的運輸費用為 ____ 元.
(2)用含x的式子表示出總運輸費(要求:列式、化簡).
(3)求總運輸費用的最大值和最小值.
(4)若這批橘子在C地和D地進行再加工,經測算,全部橘子加工完畢后總成本為w元,且w=-(x-25)2+4360.則當x= ___ 時,w有最 __ 值(填“大”或“小”).這個值是 __ .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線的頂點為A(1,4),拋物線與y軸交于點B(0,3),與x軸交于C,D兩點.點P是x軸上的一個動點.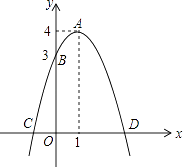
(1)求此拋物線的解析式;
(2)求C,D兩點坐標及△BCD的面積;
(3)若點P在x軸上方的拋物線上,滿足S△PCD= ![]() S△BCD , 求點P的坐標.
S△BCD , 求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD中,E是CD邊上一點,
(1)將△ADE繞點A按順時針方向旋轉,使AD,AB重合,得到△ABF,如圖1所示.觀察可知:與DE相等的線段是 , ∠AFB=∠ 
(2)如圖2,正方形ABCD中,P,Q分別是BC,CD邊上的點,且∠PAQ=45°,試通過旋轉的方式說明:DQ+BP=PQ 
(3)在(2)題中,連接BD分別交AP,AQ于M,N,你還能用旋轉的思想說明BM2+DN2=MN2 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD的邊長為2,E是CD的中點,將△ADE繞點A按順時針方向旋轉后得到△ABF,則EF的長等于( ) 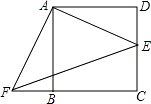
A.3
B.![]()
C.2 ![]()
D.3 ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鼓勵居民節約用水,某市自來水公司對每戶月用水量進行計費,每戶每月用水量在規定噸數以下的收費標準相同;規定噸數以上的超過部分收費標準相同,以下是小明家![]() 月份用水量和交費情況:
月份用水量和交費情況:
月份 |
|
|
|
|
|
用水量(噸) |
|
|
|
|
|
費用(元) |
|
|
|
|
|
根據表格中提供的信息,回答以下問題:
![]() 求出規定噸數和兩種收費標準;
求出規定噸數和兩種收費標準;
![]() 若小明家
若小明家![]() 月份用水
月份用水![]() 噸,則應繳多少元?
噸,則應繳多少元?
![]() 若小明家
若小明家![]() 月份繳水費
月份繳水費![]() 元,則
元,則![]() 月份用水多少噸?
月份用水多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,BC是圓O的直徑,點A,F在圓O上,連接AB,BF. 
(1)如圖1,若點A、F把半圓三等分,連接OA,OA與BF交于點E.求證:E為OA的中點;
(2)如圖2,若點A為弧 ![]() 的中點,過點A作AD⊥BC,垂足為點D,AD與BF交于點G.求證:AG=BG.
的中點,過點A作AD⊥BC,垂足為點D,AD與BF交于點G.求證:AG=BG.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,一次函數y=x+2的圖象交y軸于點A,交x軸于點B,點E在x軸的正半軸上,OE=8,點F在射線BA上,過點F作x軸的垂線,點D為垂足,OD=6.
(1)寫出點F的坐標 ;
(2)求證:∠ABO=45°;
(3)操作:將一塊足夠大的三角板的直角頂點放在線段BF的中點M處,一直角邊過點E,交FD于點C,另一直角邊與x軸相交于點N,如圖2,求點N的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,下面不能判斷是平行四邊形的是( )

A. ∠B=∠D,∠A=∠C;
B. AB∥CD,AD∥BC
C. ∠B+∠DAB=180°,∠B+∠BCD=180°
D. AB∥CD,AB=CD
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com