Question

【題目】已知拋物線頂點坐標為（1，3），且過點A（2，1）．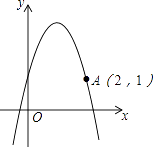

（1）求拋物線解析式；
（2）若拋物線與x軸兩交點分別為點B、C，求線段BC的長度．

Answer 1

【答案】
（1）解：設拋物線解析式為y=a（x﹣1）2+3，

把A（2，1）代入得a（2﹣1）2+3=1，解得a=﹣2，

所以拋物線解析式為y=﹣2（x﹣1）2+3

（2）解：y=0時，﹣2（x﹣1）2+3=0，

解得x1=1+ ，x2=1﹣ ，

所以BC=1+ ﹣（1﹣ ）=

【解析】（1）由于已知頂點坐標，則可設頂點式y=a（x﹣1）2+3，然后把A點坐標代入求出a即可；（2）計算函數值為0時的自變量的值，得到拋物線與x軸交點的橫坐標，然后計算兩點間的距離即可．
【考點精析】解答此題的關鍵在于理解拋物線與坐標軸的交點的相關知識，掌握一元二次方程的解是其對應的二次函數的圖像與x軸的交點坐標．因此一元二次方程中的b2-4ac，在二次函數中表示圖像與x軸是否有交點．當b2-4ac>0時，圖像與x軸有兩個交點；當b2-4ac=0時，圖像與x軸有一個交點；當b2-4ac<0時，圖像與x軸沒有交點．