
【題目】已知, ![]() 、
、![]() 均為等邊三角形,點
均為等邊三角形,點![]() 是
是![]() 內的點
內的點
(1)如圖①,說明![]() 的理由;
的理由;

(2)如圖②,當點![]() 在線段
在線段![]() 上時,求
上時,求![]() 的度數;
的度數;

(3)當![]() 為等腰直角三角形時,
為等腰直角三角形時,![]() ________度(直接寫出客案).
________度(直接寫出客案).
【答案】(1)見解析;(2)見解析;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)先理由等邊三角形的性質得出![]() ,
,![]() ,
,![]() ,即可得出結論;
,即可得出結論;
(2)同(1)得![]() ,再判斷出
,再判斷出![]() ,進而求出
,進而求出![]() ,即可得出結論;
,即可得出結論;
(3)當![]() 為等腰直角三角形時,有三種情況:I.當∠EDB=90°,DE=DB時, II.當∠BED=90°,BE=DB時,當∠EDB=90°,DE=DB時,分別作出圖形,然后根據等腰三角形性質即可求出.
為等腰直角三角形時,有三種情況:I.當∠EDB=90°,DE=DB時, II.當∠BED=90°,BE=DB時,當∠EDB=90°,DE=DB時,分別作出圖形,然后根據等腰三角形性質即可求出.
解:(1)∵![]() 和
和![]() 都是等邊三角形(已知)
都是等邊三角形(已知)
∴![]() ,
,![]() ,
,![]() (等邊三角形的性質)。
(等邊三角形的性質)。
∴![]() (等式性質),即
(等式性質),即![]() ,
,
在![]() 和
和![]() 中,
中,
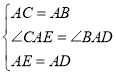 ,
,
∴![]()
∴![]() (全等三角形對應邊相等)
(全等三角形對應邊相等)
(2)∵![]() 是等邊三角形(已知)。
是等邊三角形(已知)。
∴![]() (等邊三角形的性質)。
(等邊三角形的性質)。
∴![]() (鄰補角的意義)
(鄰補角的意義)
∴![]() (等式性質)
(等式性質)
∴同理(1)得![]()
∴![]() (全等三角形對應角相等)
(全等三角形對應角相等)
∴![]() (等式性質)
(等式性質)
(3)當![]() 為等腰直角三角形時,有三種情況:
為等腰直角三角形時,有三種情況:
I.當∠EDB=90°,DE=DB時,如圖③-1:

∵∠ADE=60°,
∴∠ADB=∠ADE+∠EDB=60°+90°=150°,
又∵AD=DE,
∴AD=BD,
∴∠DAB=∠ABD=![]() ;
;
II.當∠BED=90°,BE=DB時,如圖③-2:
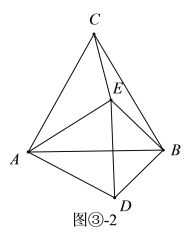
在△ABE和△ADB中:
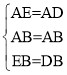 ,
,
∴△ABE≌△ADB(SSS)
∴∠ABE=∠ABD,
∴ ![]() ;
;
III.當∠EDB=90°,DE=DB時,如圖③-3:

同I可得:∠ABE=15°,
∵∠EBD=![]() ,
,
∴∠ABD=![]() .
.
綜上所述:∠ABD=![]() 或
或![]() 或
或![]() .
.
故答案為:![]() 或
或![]() 或
或![]() .
.


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點A表示的數為6,B是數軸上在A左側的一點,且A,B兩點間的距離為10.動點P從點A出發,以每秒6個單位長度的速度沿數軸向左勻速運動,設運動時間為t(t>0)秒.
(1)數軸上點B表示的數是 ,點P表示的數是 (用含t的代數式表示);
(2)動點Q從點B出發,以每秒4個單位長度的速度沿數軸向左勻速運動,若點P、Q同時出發.求:
①當點P運動多少秒時,點P與點Q相遇?
②當點P運動多少秒時,點P與點Q間的距離為8個單位長度?
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】底邊長為6厘米,高為9厘米的等腰三角形20個,迭放如圖:
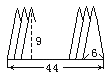
每兩個等腰三角形有等距離的間隔,底邊迭合在一起的長度是44厘米.回答下列問題:
(1)兩個三角形的間隔距離;
(2)三個三角形重迭(兩次)部分的面積之和;
(3)只有兩個三角形重迭(一次)部分的面積之和;
(4)迭到一起的總面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖,△ABC內接于⊙O,AB=AC,∠BAC=36°,AB、AC的中垂線分別交⊙O于點E、F,證明:五邊形AEBCF是⊙O的內接正五邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 在平面直角坐標系中.
在平面直角坐標系中.

(1)寫出![]() 、
、![]() 、
、![]() 三點的坐標:
三點的坐標:
![]() ( ),
( ),![]() ( ),
( ),![]() ( );
( );
(2)![]() 的面積為_______.
的面積為_______.
(3)聯結![]() ,在平面直角坐標系中找一個點
,在平面直角坐標系中找一個點![]() ,使
,使![]() 為等腰直角三角形,且以
為等腰直角三角形,且以![]() 為直角邊,則
為直角邊,則![]() 的坐標是________(直接寫答案).
的坐標是________(直接寫答案).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】家用電滅蚊器的發熱部分使用了PTC發熱材料,它的電阻R(kΩ)隨溫度t(℃)(在一定范圍內)變化的大致圖象如圖所示.通電后,發熱材料的溫度在由室溫10℃上升到30℃的過程中,電阻與溫度成反比例關系,且在溫度達到30℃時,電阻下降到最小值;隨后電阻隨溫度升高而增加,溫度每上升1℃,電阻增加![]() kΩ.
kΩ.
(1)求當10≤t≤30時,R和t之間的關系式;
(2)求溫度在30℃時電阻R的值;并求出t≥30時,R和t之間的關系式;
(3)家用電滅蚊器在使用過程中,溫度在什么范圍內時,發熱材料的電阻不超過6 kΩ?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市高中招生體育考試前教育部門為了解全市九年級男生考試項目的選擇情況(每人限選一項),對全市部分九年級男生進行了調查,將調查結果分成五類:A、實心球(2kg);B、立定跳遠;C、50米跑;D、半場運球;E、其它.并將調查結果繪制成以下兩幅不完整的統計圖,請你根據統計圖解答下列問題:

(1)將上面的條形統計圖補充完整;
(2)假定全市九年級畢業學生中有5500名男生,試估計全市九年級男生中選“50米跑”的人數有多少人?
(3)甲、乙兩名九年級男生在上述選擇率較高的三個項目:B、立定跳遠;C、50米跑;D、半場運球中各選一項,同時選擇半場運球和立定跳遠的概率是多少?請用列表法或畫樹形圖的方法加以說明并列出所有等可能的結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數軸上兩點間的距離等于這兩個點所對應的數的差的絕對值.例:點A、B在數軸上對應的數分別為a、b,則A、B兩點間的距離表示為AB=|a﹣b|.根據以上知識解題:
(1)點A在數軸上表示3,點B在數軸上表示2,那么AB=_______.
(2)在數軸上表示數a的點與﹣2的距離是3,那么a=______.
(3)如果數軸上表示數a的點位于﹣4和2之間,那么|a+4|+|a﹣2|=______.
(4)對于任何有理數x,|x﹣3|+|x﹣6|是否有最小值?如果有,直接寫出最小值.如果沒有.請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是“作圓的內接正方形”的尺規作圖過程。
已知:⊙O.
求作:圓的內接正方形.
如圖,
(1)過圓心O作直線AC,與⊙O相交于A,C兩點;
(2)過點O作直線BD⊥AC,交⊙O于B,D兩點;
(3)連接AB,BC,CD,DA。
∴四邊形ABCD為所求。
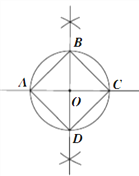
請回答:該尺規作圖的依據是____________________________。(寫出兩條)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com