
【題目】在平面直角坐標系xOy中,函數![]() (x>0)的圖象與直線l1:
(x>0)的圖象與直線l1:![]() 交于點A,與直線l2:x=k交于點B.直線l1與l2交于點C.
交于點A,與直線l2:x=k交于點B.直線l1與l2交于點C.

(1) 當點A的橫坐標為1時,則此時k的值為 _______;
(2) 橫、縱坐標都是整數的點叫做整點. 記函數![]() (x>0) 的圖像在點A、B之間的部分與線段AC,BC圍成的區域(不含邊界)為W.
(x>0) 的圖像在點A、B之間的部分與線段AC,BC圍成的區域(不含邊界)為W.
①當k=3時,結合函數圖像,則區域W內的整點個數是_________;
②若區域W內恰有1個整點,結合函數圖象,直接寫出k的取值范圍:___________.
科目:初中數學 來源: 題型:
【題目】問題提出
如圖①,![]() 、
、![]() 是⊙
是⊙![]() 的兩條弦,
的兩條弦, ![]() ,
, ![]() 是
是![]() 的中點,
的中點, ![]() ,垂足為
,垂足為![]() .
.
求證: ![]() .
.


小敏在解答此題時,利用了“補短法”進行證明,她的方法如下:
如圖②,延長![]() 至
至![]() ,使
,使![]() ,連接
,連接![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
(請你在下面的空白處完成小敏的證明過程.)
推廣運用
如圖③,等邊![]() 內接于⊙
內接于⊙![]() ,
, ![]() .
. ![]() 是
是![]() 上一點,
上一點, ![]() ,
, ![]() ,垂足為
,垂足為![]() ,則
,則![]() 的周長是__________.
的周長是__________.


拓展研究
如圖④,若將“問題提出”中的“![]() 是
是![]() 的中點”改成“
的中點”改成“![]() 是
是![]() 的中點”,其余條件不變,“
的中點”,其余條件不變,“![]() ”這一結論還成立嗎?若成立,請說明理由;若不成立,寫出
”這一結論還成立嗎?若成立,請說明理由;若不成立,寫出![]() 、
、![]() 、
、![]() 三者之間存在的關系并說明理由.
三者之間存在的關系并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一個可以自由轉動的轉盤被平均分成3個扇形,分別標有1,2,3三個數字.小王和小李各轉動一次轉盤為一次游戲,當每次轉盤停止后,指針所指扇形內的數為各自所得的數,一次游戲結束后得到一組數(若指針指在分界線時重轉).
(1)請你用樹狀圖或列表的方法表示出每次游戲可能出現的所有結果;
(2)求每次游戲后得到的一組數恰好是方程x2﹣4x+3=0的解的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CB=CA,∠ACB=90°,點D在邊BC上(與B,C不重合),四邊形ADEF為正方形,過點F作FG⊥CA,交CA的延長線于點G,連接FB,交DE于點Q,給出以下結論:①AC=FG;②S△FAB∶S四邊形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正確結論的個數是( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(6分)△ABC與△A′B′C′在平面直角坐標系中的位置如圖.

(1)分別寫出下列各點的坐標:A′ ; B′ ;C′ ;
(2)說明△A′B′C′由△ABC經過怎樣的平移得到? .
(3)若點P(a,b)是△ABC內部一點,則平移后△A′B′C′內的對應點P′的坐標為 ;
(4)求△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,有若干個整數點,其順序按圖中“→”方向排列,如(0,1),(0,2),(1,2),(1,3),(0,3),(﹣1,3)…,根據這個規律探索可得,第90個點的坐標為_____.
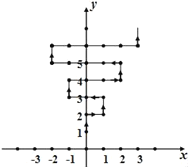
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在邊長為a的正方形中挖去一個邊長為b的小正方形(a>b)(如圖甲),把余下的部分拼成一個長方形(如圖乙),根據兩個圖形中陰影部分的面積相等,可以驗證( )
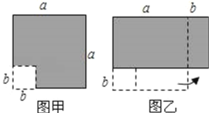
A. (a+2b)(a﹣b)=a2+ab﹣2b2
B. a2﹣b2=(a+b)(a﹣b)
C. (a+b)2=a2+2ab+b2
D. (a﹣b)2=a2﹣2ab+b2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在正方形ABCD中,以AB為邊向正方形外作等邊三角形ABE,連接CE、BD交于點G,連接AG,那么∠AGD的底數是______度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】函數 yl= x ( x ≥0 ) , ![]() ( x > 0 )的圖象如圖所示,則結論: ① 兩函數圖象的交點A的坐標為(3 ,3 ) ② 當 x > 3
( x > 0 )的圖象如圖所示,則結論: ① 兩函數圖象的交點A的坐標為(3 ,3 ) ② 當 x > 3 ![]() 時, ③ 當 x =1時, BC = 8
時, ③ 當 x =1時, BC = 8
④ 當 x 逐漸增大時, yl 隨著 x 的增大而增大,y2隨著 x 的增大而減小.其中正確結論的序號是_ .
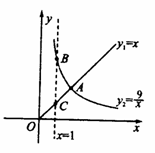
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com