
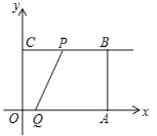
【題目】已知:如圖所示,在平面直角坐標(biāo)系![]() 中,四邊形
中,四邊形![]() 是矩形,
是矩形,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發(fā),沿射線
出發(fā),沿射線![]() 方向以每秒2個單位長度的速度運動;同時,動點
方向以每秒2個單位長度的速度運動;同時,動點![]() 從點
從點![]() 出發(fā),沿
出發(fā),沿![]() 軸正半軸方向以每秒1個單位長度的速度運動,設(shè)點
軸正半軸方向以每秒1個單位長度的速度運動,設(shè)點![]() 、點
、點![]() 的運動時間為
的運動時間為![]()
(1)當(dāng)![]() 時,求經(jīng)過點
時,求經(jīng)過點![]() ,
,![]() ,
,![]() 三點的拋物線的解析式;
三點的拋物線的解析式;
(2)當(dāng)![]() 時,求
時,求![]() 的值;
的值;
(3)當(dāng)線段![]() 與線段
與線段![]() 相交于點
相交于點![]() ,且
,且![]() 時,求
時,求![]() 的值;
的值;
(4)連接![]() ,當(dāng)點
,當(dāng)點![]() ,
,![]() 在運動過程中,記△
在運動過程中,記△![]() 與矩形
與矩形![]() 重疊部分的面積為
重疊部分的面積為![]() ,求
,求![]() 與
與![]() 的函數(shù)關(guān)系式
的函數(shù)關(guān)系式
【答案】(1)y=﹣![]() x2+3x;(2)
x2+3x;(2)![]() ;(3)t為3s;(4)S=
;(3)t為3s;(4)S=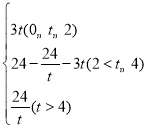
【解析】
(1)可求得P點坐標(biāo),由O、P、A的坐標(biāo),利用待定系數(shù)法可求得拋物線解析式;
(2)當(dāng)t=2s時,可知P與點B重合,在Rt△ABQ中可求得tan∠QPA的值;
(3)用t可表示出BP和AQ的長,由△PBM∽△QAM可得到關(guān)于t的方程,可求得t的值;
(4)當(dāng)點Q在線段OA上時,S=S△CPQ;當(dāng)點Q在線段OA上,且點P在線段CB的延長線上時,由相似三角形的性質(zhì)可用t表示出AM的長,由S=S四邊形BCQM=S矩形OABCS△COQS△AMQ,可求得S與t的關(guān)系式;當(dāng)點Q在OA的延長線上時,設(shè)CQ交AB于點M,利用△AQM∽△BCM可用t表示出AM,從而可表示出BM,S=S△CBM,可求得答案.
解:(1)當(dāng)t=1s時,則CP=2,
∵OC=3,四邊形OABC是矩形,
∴P(2,3),且A(4,0),
∵拋物線過原點O,
∴可設(shè)拋物線解析式為y=ax2+bx,
∴![]() ,解得
,解得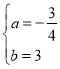 ,
,
∴過O、P、A三點的拋物線的解析式為y=﹣![]() x2+3x;
x2+3x;
(2)當(dāng)t=2s時,則CP=2×2=4=BC,即點P與點B重合,OQ=2,如圖1,
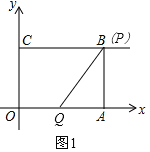
∴AQ=OA﹣OQ=4﹣2=2,且AP=OC=3,
∴tan∠QPA=![]() =
=![]() ;
;
(3)當(dāng)線段PQ與線段AB相交于點M,則可知點Q在線段OA上,點P在線段CB的延長線上,如圖2,
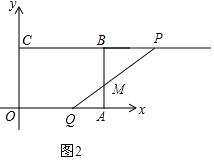
則CP=2t,OQ=t,
∴BP=PC﹣CB=2t﹣4,AQ=OA﹣OQ=4﹣t,
∵PC∥OA,
∴△PBM∽△QAM,
∴![]() ,且BM=2AM,
,且BM=2AM,
∴![]() =2,解得t=3,
=2,解得t=3,
∴當(dāng)線段PQ與線段AB相交于點M,且BM=2AM時,t為3s;
(4)當(dāng)0≤t≤2時,如圖3,

由題意可知CP=2t,
∴S=S△PCQ=![]() ×2t×3=3t;
×2t×3=3t;
當(dāng)2<t≤4時,設(shè)PQ交AB于點M,如圖4,
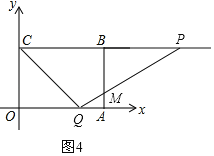
由題意可知PC=2t,OQ=t,則BP=2t﹣4,AQ=4﹣t,
同(3)可得![]() =
=![]() ,
,
∴BM=![]() AM,
AM,
∴3﹣AM=![]() AM,解得AM=
AM,解得AM=![]() ,
,
∴S=S四邊形BCQM=S矩形OABC﹣S△COQ﹣S△AMQ=3×4﹣![]() ×t×3﹣
×t×3﹣![]() ×(4﹣t)×
×(4﹣t)×![]() =24﹣
=24﹣![]() ﹣3t;
﹣3t;
當(dāng)t>4時,設(shè)CQ與AB交于點M,如圖5,
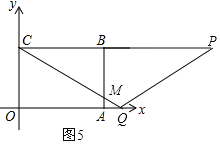
由題意可知OQ=t,AQ=t﹣4,
∵AB∥OC,
∴![]() ,即
,即![]() =
=![]() ,解得AM=
,解得AM=![]() ,
,
∴BM=3﹣![]() ,
,
∴S=S△BCM=![]() ×4×
×4×![]() ;
;
綜上可知S=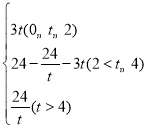 .
.


科目:初中數(shù)學(xué) 來源: 題型:
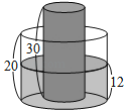
【題目】如圖,有一內(nèi)部裝有水的直圓柱形水桶,桶高![]() ;另有一直圓柱形的實心鐵柱,柱高
;另有一直圓柱形的實心鐵柱,柱高![]() ,直立放置于水桶底面上,水桶內(nèi)的水面高度為
,直立放置于水桶底面上,水桶內(nèi)的水面高度為![]() ,且水桶與鐵柱的底面半徑比為
,且水桶與鐵柱的底面半徑比為![]() .今小賢將鐵柱移至水桶外部,過程中水桶內(nèi)的水量未改變,若不計水桶厚度,則水桶內(nèi)的水面高度變?yōu)椋?/span> )
.今小賢將鐵柱移至水桶外部,過程中水桶內(nèi)的水量未改變,若不計水桶厚度,則水桶內(nèi)的水面高度變?yōu)椋?/span> )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,方格紙中的每個小方格都是邊長為1個單位的正方形.Rt△ABC的頂點均在格點上,建立平面直角坐標(biāo)系后,點A的坐標(biāo)為(﹣4,1),點B的坐標(biāo)為(﹣1,1).
(1)先將Rt△ABC向右平移5個單位,再向下平移1個單位后得到Rt△A1B1C1.試在圖中畫出圖形Rt△A1B1C1,并寫出A1的坐標(biāo);
(2)將Rt△A1B1C1繞點A1順時針旋轉(zhuǎn)90°后得到Rt△A2B2C2,試在圖中畫出圖形Rt△A2B2C2.并計算Rt△A1B1C1在上述旋轉(zhuǎn)過程中C1所經(jīng)過的路程.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下面是小東設(shè)計的“過圓外一點作這個圓的兩條切線”的尺規(guī)作圖過程.
已知:⊙O及⊙O外一點P.
求作:直線PA和直線PB,使PA切⊙O于點A,PB切⊙O于點B.
作法:如圖,
①連接OP,分別以點O和點P為圓心,大于![]() OP的同樣長為半徑作弧,兩弧分別交于點M,N;
OP的同樣長為半徑作弧,兩弧分別交于點M,N;
②連接MN,交OP于點Q,再以點Q為圓心,OQ的長為半徑作弧,交⊙O于點A和點B;
③作直線PA和直線PB.
所以直線PA和PB就是所求作的直線.
根據(jù)小東設(shè)計的尺規(guī)作圖過程,
(1)使用直尺和圓規(guī),補全圖形;(保留作圖痕跡)
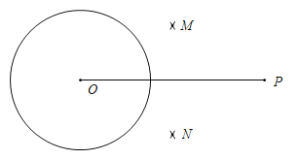
(2)完成下面的證明.
證明:∵OP是⊙Q的直徑,
∴ ∠OAP=∠OBP=________°( )(填推理的依據(jù)).
∴PA⊥OA,PB⊥OB.
∵OA,OB為⊙O的半徑,
∴PA,PB是⊙O的切線.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
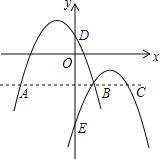
【題目】拋物線![]() 的部分圖象如圖所示,與x軸的一個交點坐標(biāo)為
的部分圖象如圖所示,與x軸的一個交點坐標(biāo)為![]() ,拋物線的對稱軸是
,拋物線的對稱軸是![]() 下列結(jié)論中:
下列結(jié)論中:
![]() ;
;![]() ;
;![]() 方程
方程![]() 有兩個不相等的實數(shù)根;
有兩個不相等的實數(shù)根;![]() 拋物線與x軸的另一個交點坐標(biāo)為
拋物線與x軸的另一個交點坐標(biāo)為![]() ;
;![]() 若點
若點![]() 在該拋物線上,則
在該拋物線上,則![]() .
.
其中正確的有![]()
![]()

A. 5個 B. 4個 C. 3個 D. 2個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為響應(yīng)荊州市“創(chuàng)建全國文明城市”號召,某單位不斷美化環(huán)境,擬在一塊矩形空地上修建綠色植物園,其中一邊靠墻,可利用的墻長不超過18m,另外三邊由36m長的柵欄圍成.設(shè)矩形ABCD空地中,垂直于墻的邊AB=xm,面積為ym2(如圖).
(1)求y與x之間的函數(shù)關(guān)系式,并寫出自變量x的取值范圍;
(2)若矩形空地的面積為160m2,求x的值;
(3)若該單位用8600元購買了甲、乙、丙三種綠色植物共400棵(每種植物的單價和每棵栽種的合理用地面積如下表).問丙種植物最多可以購買多少棵?此時,這批植物可以全部栽種到這塊空地上嗎?請說明理由.
甲 | 乙 | 丙 | |
單價(元/棵) | 14 | 16 | 28 |
合理用地(m2/棵) | 0.4 | 1 | 0.4 |

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC內(nèi)接于⊙O,∠CBG=∠A,CD為直徑,OC與AB相交于點E,過點E作EF⊥BC,垂足為F,延長CD交GB的延長線于點P,連接BD.
(1)求證:PG與⊙O相切;
(2)若![]() =
=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的條件下,若⊙O的半徑為8,PD=OD,求OE的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,拋物線l1:y1=a(x+1)2+2與l2:y2=﹣(x﹣2)2﹣1交于點B(1,﹣2),且分別與y軸交于點D、E.過點B作x軸的平行線,交拋物線于點A、C,則以下結(jié)論:
①無論x取何值,y2總是負數(shù);
②l2可由l1向右平移3個單位,再向下平移3個單位得到;
③當(dāng)﹣3<x<1時,隨著x的增大,y1﹣y2的值先增大后減小;
④四邊形AECD為正方形.
其中正確的是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
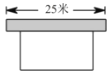
【題目】如圖,要建一個長方形養(yǎng)雞場,養(yǎng)雞場的一邊靠墻(墻長25米),另三邊用竹籬笆圍成,竹籬笆的長為40米,若要圍成的養(yǎng)雞場的面積為180平方米,求養(yǎng)雞場的長、寬各為多少米,設(shè)與墻平行的一邊長為![]() 米.
米.
(1)填空:(用含![]() 的代數(shù)式表示)另一邊長為 米;
的代數(shù)式表示)另一邊長為 米;
(2)列出方程,并求出問題的解.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com