
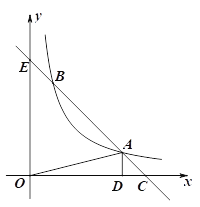
【題目】如圖,已知函數(shù)![]() 的圖象與一次函數(shù)
的圖象與一次函數(shù)![]() 的圖象相交不同的點(diǎn)A、B,過點(diǎn)A作AD⊥
的圖象相交不同的點(diǎn)A、B,過點(diǎn)A作AD⊥![]() 軸于點(diǎn)D,連接AO,其中點(diǎn)A的橫坐標(biāo)為
軸于點(diǎn)D,連接AO,其中點(diǎn)A的橫坐標(biāo)為![]() ,△AOD的面積為2.
,△AOD的面積為2.
(1)求![]() 的值及
的值及![]() =4時
=4時![]() 的值;
的值;
(2)記![]() 表示為不超過
表示為不超過![]() 的最大整數(shù),例如:
的最大整數(shù),例如:![]() ,
,![]() ,設(shè)
,設(shè)![]() ,若
,若![]() ,求
,求![]() 值
值
【答案】(1)4;1;(2)5.
【解析】(1)設(shè)A(x0,y0),可表示出△AOD的面積,再結(jié)合x0y0=k可求得k的值,根據(jù)A的橫坐標(biāo)可得縱坐標(biāo),代入一次函數(shù)可得m的值;
(2)先根據(jù)一次函數(shù)與x軸的交點(diǎn)確定OC的長,表示DC的長,從而可以表示t,根據(jù)A的橫坐標(biāo)為x0,即x0滿足![]() =mx+5,可得:mx02+5x0=4,再根據(jù)m的取值計(jì)算m2t,最后利用新定義可得結(jié)論.
=mx+5,可得:mx02+5x0=4,再根據(jù)m的取值計(jì)算m2t,最后利用新定義可得結(jié)論.
(1)設(shè)A(x0,y0),則OD=x0,AD=y0,
∴S△AOD=![]() ODAD=
ODAD=![]() x0y0=2,
x0y0=2,
∴k=x0y0=4;
當(dāng)x0=4時,y0=1,
∴A(4,1),
代入y=mx+5中得4m+5=1,m=-1;
(2)∵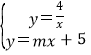 ,
,
∴![]() =mx+5,整理得,mx2+5x-4=0,
=mx+5,整理得,mx2+5x-4=0,
∵A的橫坐標(biāo)為x0,
∴mx02+5x0=4,
當(dāng)y=0時,mx+5=0,
x=-![]() ,
,
∵OC=-![]() ,OD=x0,
,OD=x0,
∴m2t=m2(ODDC),
=m2x0(-![]() -x0),
-x0),
=m(-5x0-mx02),
=-4m,
∵-![]() <m<-
<m<-![]() ,
,
∴5<-4m<6,
∴[m2t]=5.


 出彩同步大試卷系列答案
出彩同步大試卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖①,點(diǎn)O是線段AD上一動點(diǎn)(不與點(diǎn)A、D重合),分別以AO和DO為邊在AD的同側(cè)作等邊三角形OAB和等邊三角形OCD,連結(jié)AC、BD相交于點(diǎn)E,連結(jié)OE.
(1)當(dāng)點(diǎn)O為AD的中點(diǎn)時,求∠DEA的度數(shù);
(2)在(1)的條件下,△ADE是軸對稱圖形嗎?如果是,指出它的對稱軸;如果不是,說明理由;
(3)當(dāng)點(diǎn)O不在AD的中點(diǎn)時,求證EO平分∠DEA.


圖① 圖②
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】△ABC 中,AB=AC,過其中一個頂點(diǎn)的直線可以把這個三角形分成另外兩個等腰三角形,則∠BAC( )
A. 36°,90°,![]() , 108°B. 36°,72°,
, 108°B. 36°,72°,![]() ,90°
,90°
C. 90°,72°,108°,![]() D. 36°,90°,108°,
D. 36°,90°,108°,![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,每一幅圖中都有若干個大小不同的四邊形,第1幅圖中有1個四邊形,第2幅圖中有3個四邊形,第3幅圖中有5個四邊形

(1)第4幅圖中有 個四邊形,第5幅圖中有 個四邊形;
(2)根據(jù)第1幅圖到第5幅圖的規(guī)律,推測第![]() 幅圖中有 個四邊形;(用含字母
幅圖中有 個四邊形;(用含字母![]() 的代數(shù)式表示)
的代數(shù)式表示)
(3)根據(jù)(2)的推測,請你計(jì)算第![]() 幅圖中四邊形的個數(shù)比第
幅圖中四邊形的個數(shù)比第![]() 幅圖中四邊形個數(shù)多幾個?
幅圖中四邊形個數(shù)多幾個?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:A=2x2+3xy![]() 5x+1,B=
5x+1,B=![]() x2+xy+2
x2+xy+2
(1)求A+2B.
(2)若A+2B的值與x的值無關(guān),求y的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,利用關(guān)于坐標(biāo)系軸對稱的點(diǎn)的坐標(biāo)的特點(diǎn).
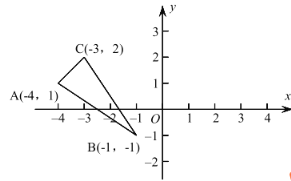
(1)畫出與△ABC 關(guān)于 y 軸對稱的圖形△A1B1C1;
(2)寫出各點(diǎn)坐標(biāo):△A1( ),B1( ),C1 ( ).
(3)直接寫出△ABC 的面積______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
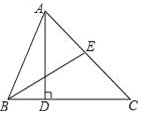
【題目】如圖,AD為△ABC的高,BE為△ABC的角平分線,若∠EBA=32°,∠AEB=70°.
(1)求∠CAD的度數(shù);
(2)若點(diǎn)F為線段BC上任意一點(diǎn),當(dāng)△EFC為直角三角形時,則∠BEF的度數(shù)為
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
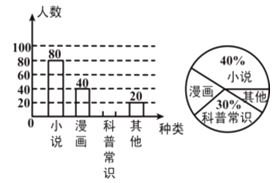
【題目】某校為了了解本校七年級學(xué)生課外閱讀的喜好,隨機(jī)抽取該校七年級部分學(xué)生進(jìn)行問卷調(diào)査(每人只選一種書籍).下圖是整理數(shù)據(jù)后繪制的兩幅不完整的統(tǒng)計(jì)圖,請你根據(jù)圖中提供的信息解答下列問題:
(1)在扇形統(tǒng)計(jì)圖中,“其他”所在扇形的圓心角等于 度;
(2)若該年級有600名學(xué)生,請你估計(jì)該年級喜歡“科普常識”的學(xué)生人數(shù)約是 .
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com