
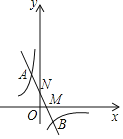
【題目】如圖,AB為半圓O的直徑,點C在半圓上,過點O作BC的平行線交AC于點E,交過點A的直線于點D,且∠D=∠BAC
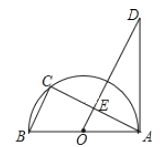
(1)求證:AD是半圓O的切線;
(2)求證:△ABC∽△DOA;
(3)若BC=2,CE=![]() ,求AD的長.
,求AD的長.
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)要證AD是半圓O的切線只要證明∠DAO=90°即可;
(2)根據兩組角對應相等的兩個三角形相似即可得證;
(3)先求出AC、AB、AO的長,由第(2)問的結論△ABC∽△DOA,根據相似三角形的性質:對應邊成比例可得到AD的長.
(1)證明:∵AB為直徑,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=∠ACB=90°,
∴∠AOD+∠BAC=90°,
又∵∠D=∠BAC,
∴∠AOD+∠D=90°,
∴∠OAD=90°,
∴AD⊥OA,
∴AD是半圓O的切線;
(2)證明:由(1)得∠ACB=∠OAD=90°,
又∵∠D=∠BAC,
∴△ABC∽△DOA;
(3)解:∵O為AB中點,OD∥BC,
∴OE是△ABC的中位線,則E為AC中點,
∴AC=2CE,
∵BC=2,CE=![]() ,
,
∴AC=![]()
∴AB=![]() ,
,
∴OA=![]() AB=
AB=![]() ,
,
由(2)得:△ABC∽△DOA,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.


科目:初中數學 來源: 題型:
【題目】已知∠MON=120°,點A,B分別在ON,OM邊上,且OA=OB,點C在線段OB上(不與點O,B重合),連接CA.將射線CA繞點C逆時針旋轉120°得到射線CA′,將射線BO繞點B逆時針旋轉150°與射線CA′交于點D.

(1)根據題意補全圖1;
(2)求證:
①∠OAC=∠DCB;
②CD=CA(提示:可以在OA上截取OE=OC,連接CE);
(3)點H在線段AO的延長線上,當線段OH,OC,OA滿足什么等量關系時,對于任意的點C都有∠DCH=2∠DAH,寫出你的猜想并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某企業為響應國家教育扶貧的號召,決定對某鄉鎮全體貧困初、高中學生進行資助,初中學生每月資助200元,高中學生每月資助300元.已知該鄉受資助的初中學生人數是受資助的高中學生人數的2倍,且該企業在2018年下半年7﹣12月這6個月資助學生共支出10.5萬元.
(1)問該鄉鎮分別有多少名初中學生和高中學生獲得了資助?
(2)2018年7﹣12月期間,受資助的初、高中學生中,分別有30%和40%的學生被評為優秀學生,從而獲得了該鄉鎮政府的公開表揚.同時,提供資助的企業為了激發更多受資助學生的進取心和學習熱情,決定對2019年上半年1﹣6月被評為優秀學生的初中學生每人每月增加a%的資助,對被評為優秀學生的高中學生每人每月增加2a%的資助.在此獎勵政策的鼓勵下,2019年1﹣6月被評為優秀學生的初、高中學生分別比2018年7﹣12月的人數增加了3a%、a%.這樣,2019年上半年評為優秀學生的初、高中學生所獲得的資助總金額一個月就達到了10800元,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+bx﹣1(a≠0)交x軸于A,B(1,0)兩點,交y軸于點C,一次函數y=x+3的圖象交坐標軸于A,D兩點,E為直線AD上一點,作EF⊥x軸,交拋物線于點F
(1)求拋物線的解析式;
(2)若點F位于直線AD的下方,請問線段EF是否有最大值?若有,求出最大值并求出點E的坐標;若沒有,請說明理由;
(3)在平面直角坐標系內存在點G,使得G,E,D,C為頂點的四邊形為菱形,請直接寫出點G的坐標.
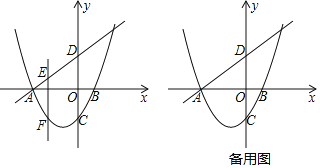
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=ax2+2x+c(a<0)與x軸交于點A和點B(點A在原點的左側,點B在原點的右側),與y軸交于點C,OB=OC=3.
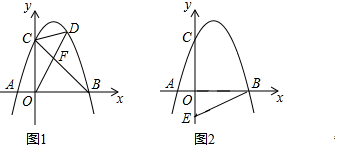
(1)求該拋物線的函數解析式;
(2)如圖1,連接BC,點D是直線BC上方拋物線上的點,連接OD,CD,OD交BC于點F,當S△COF:S△CDF=3:2時,求點D的坐標.
(3)如圖2,點E的坐標為(0,![]() ),在拋物線上是否存在點P,使∠OBP=2∠OBE?若存在,請直接寫出符合條件的點P的坐標;若不存在,請說明理由.
),在拋物線上是否存在點P,使∠OBP=2∠OBE?若存在,請直接寫出符合條件的點P的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的不等式組![]() 的整數解個數不少于3個,但不多于5個,且關于y的分式方程
的整數解個數不少于3個,但不多于5個,且關于y的分式方程![]() 的解為整數,則符合條件的所有整數m的和為( )
的解為整數,則符合條件的所有整數m的和為( )
A.﹣24B.﹣19C.﹣16D.﹣10
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x函數y=|﹣x2+bx﹣7|﹣4,點(4,5)在函數上,且b為整數,根據我們已有的研究函數的經驗,請對該函數及其圖象進行如下探究,并完成以下問題:
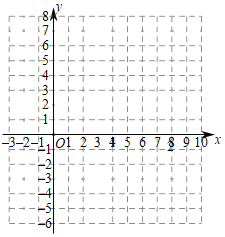
(1)求b= ;
(2)函數圖象探究:
①下表是y與x的幾組對應值,請直接寫出m與n的值:m= ,n= ;
x | … | ﹣ | 0 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 7 | 8 | 8 | … |
y | … | m | 3 |
| ﹣4 | 1 | 4 | n | 4 | 1 | ﹣4 |
| 3 | 5 | … |
②根據你喜歡的方式,在如圖所示的平面直角坐標系中,畫出該函數圖象;
(3)結果函數圖象,寫出該函數的一條性質: ;
(4)若關于x的方程|﹣x2+bx﹣7|=m+4有四個根,則m的取值范圍為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小明設計的“在一個平行四邊形內作菱形”的尺規作圖過程.
已知:四邊形![]() 是平行四邊形.
是平行四邊形.
求作:菱形![]() (點
(點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上).
上).
作法:①以![]() 為圓心,
為圓心,![]() 長為半徑作弧,交
長為半徑作弧,交![]() 于點
于點![]() ;
;
②以![]() 為圓心,
為圓心,![]() 長為半徑作弧,交
長為半徑作弧,交![]() 于點
于點![]() ;
;
③連接![]() .所以四邊形
.所以四邊形![]() 為所求作的菱形.
為所求作的菱形.
根據小明設計的尺規作圖過程,
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:∵![]() ,
,![]() ,
,
∴ = .
在![]() 中,
中,![]() .
.
即![]() .
.
∴四邊形![]() 為平行四邊形.
為平行四邊形.
∵![]() ,
,
∴四邊形![]() 為菱形( )(填推理的依據).
為菱形( )(填推理的依據).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,關于x的一次函數y=k1x+b的圖象與反比例函數y=![]() 的圖象相交于A(﹣2,8),B(4,m)兩點.
的圖象相交于A(﹣2,8),B(4,m)兩點.
(1)求一次函數與反比例函數的解析式.
(2)設一次函數y=k1x+b的圖象與x軸,y軸的交點分別為M,N,P是x軸上一動點,當以P,M,N三點為頂點的三角形是等腰三角形時,求點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com