
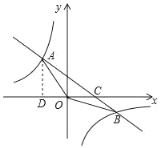
【題目】如圖,在平面直角坐標系xOy中,一次函數y=kx+b(k≠0)的圖象與反比例函數y=![]() (n≠0)的圖象交于第二、四象限內的A、B兩點與x軸交于點C,點B坐標為(m,﹣1),AD⊥x軸,且AD=3,tan∠AOD=
(n≠0)的圖象交于第二、四象限內的A、B兩點與x軸交于點C,點B坐標為(m,﹣1),AD⊥x軸,且AD=3,tan∠AOD=![]()
(1)求該反比例函數和一次函數的解析式;
(2)連接OB,求S△AOC﹣S△BOC的值;
(3)點E是x軸上一點,且△AOE是等腰三角形請直接寫出滿足條件的E點的個數(寫出個數即可,不必求出E點坐標).
【答案】(1)y=﹣![]() ,y=﹣
,y=﹣![]() x+2;(2)S△AOC﹣S△BOC=4;(3)滿足條件的點P有四個.
x+2;(2)S△AOC﹣S△BOC=4;(3)滿足條件的點P有四個.
【解析】
(1)先根據銳角三角函數求出OD,求出點A坐標,進而求出反比例函數解析式,再求出點B坐標,最后將點A,B坐標代入直線解析式中,即可得出結論;
(2)先求出點C坐標,進而用三角形的面積公式求解即可得出結論;
(3)分三種情況,利用等腰三角形的性質,建立方程求解即可得出結論.
(1)∵AD⊥x軸,
∴∠ADO=90°,
在Rt△ADO中,AD=3,tan∠AOD=![]() ,
,
∴OD=2,
∴A(﹣2,3),
∵點A在反比例函數y=![]() 的圖象上,
的圖象上,
∴n=﹣2×3=﹣6,
∴反比例函數的解析式為y=﹣![]() ,
,
∵點B(m,﹣1)在反比例函數y=﹣![]() 的圖象上,
的圖象上,
∴﹣m=﹣6,
∴m=6,
∴B(6,﹣1),
將點A(﹣2,3),B(6,﹣1)代入直線y=kx+b中,得![]() ,
,
∴ ,
,
∴一次函數的解析式為y=﹣![]() x+2;
x+2;
(2)由(1)知,A(﹣2,3),直線AB的解析式為y=﹣![]() x+2,
x+2,
令y=0,
∴﹣x+2=0,
∴x=4,
∴C(4,0),
∴S△AOC﹣S△BOC=![]() OC|yA|﹣
OC|yA|﹣![]() OC|yB|=
OC|yB|=![]() ×4(3﹣1)=4;
×4(3﹣1)=4;
(3)設E(m,0),由(1)知,A(﹣2,3),
∴OA2=13,OE2=m2,AE2=(m+2)2+9,
∵△AOE是等腰三角形,
∴①當OA=OE時,
∴13=m2,
p>∴m=±∴E(﹣![]() ,0)或(
,0)或(![]() ,0),
,0),
②當OA=AE時,13=(m+2)2+9,
∴m=0(舍)或m=4,
∴E(4,0),
③當OE=AE時,m2=(m+2)2+9,
∴m=﹣![]() ,
,
∴E(﹣![]() ,0),
,0),
即:滿足條件的點P有四個.


 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,認真觀察下面這些算式,并結合你發現的規律,完成下列問題:

(1)請寫出:
算式⑤ ;
算式⑥ ;
(2)上述算式的規律可以用文字概括為:“兩個連續奇數的平方差能被8整除”,如果設兩個連續奇數分別為![]() 和
和![]() (
(![]() 為整數),請說明這個規律是成立的;
為整數),請說明這個規律是成立的;
(3)你認為“兩個連續偶數的平方差能被8整除”這個說法是否也成立呢?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AB=20cm,AD=30cm,∠ABC=60°,點Q從點B出發沿BA向點A勻速運動,速度為2cm/s,同時,點P從點D出發沿DC向點C勻速運動,速度為3cm/s,當點P停止運動時,點Q也隨之停止運動,過點P做PM⊥AD交AD于點M,連接PQ、QM.設運動的時間為ts(0<t≤6).
(1)當PQ⊥PM時,求t的值;
(2)設△PQM的面積為y(cm2),求y與t之間的函數關系式;
(3)是否存在某一時刻t,使得△PQM的面積是ABCD面積的![]() ?若存在,求出相應t的值;若不存在,請說明理由;
?若存在,求出相應t的值;若不存在,請說明理由;
(4)過點M作MN∥AB交BC于點N,是否存在某一時刻t,使得P在線段MN的垂直平分線上?若存在,求出相應t的值;若不存在,請說明理由;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明購買A,B兩種商品,每次購買同一種商品的單價相同,具體信息如下表:
次數 | 購買數量(件 | 購買總費用(元 | |
A | B | ||
第一次 | 2 | 1 | 55 |
第二次 | 1 | 3 | 65 |
根據以上信息解答下列問題:
(1)求A,B兩種商品的單價;
(2)若第三次購買這兩種商品共12件,且A種商品的數量不少于B種商品數量的2倍,請設計出最省錢的購買方案,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
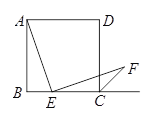
【題目】如圖,已知邊長為4的正方形ABCD,E是BC邊上一動點(與B、C不重合),連結AE,作EF⊥AE交∠BCD的外角平分線于F,設BE=x,△ECF的面積為y,下列圖象中,能表示y與x的函數關系的圖象大致是( )
A. 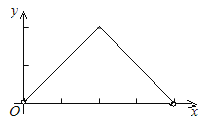 B.
B. 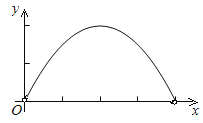
C. 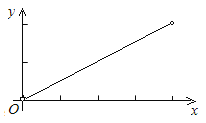 D.
D. 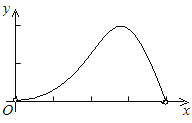
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() ,與
,與![]() 軸的一個交點坐標為
軸的一個交點坐標為![]() ,其部分圖象如圖所示.現有下列結論:①
,其部分圖象如圖所示.現有下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④當
;④當![]() 時,
時,![]() 隨
隨![]() 的增大而減小;⑤
的增大而減小;⑤![]() ;⑥
;⑥![]() .其中正確的結論有( )
.其中正確的結論有( )
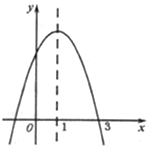
A. l個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
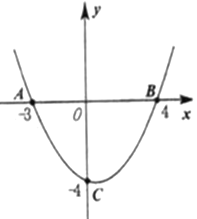
(1)求拋物線解析式:
(2)拋物線對稱軸上存在一點![]() ,連接
,連接![]() 、
、![]() ,當
,當![]() 值最大時,求點H坐標:
值最大時,求點H坐標:
(3)若拋物線上存在一點![]() ,
,![]() ,當
,當![]() 時,求點
時,求點![]() 坐標:
坐標:
(4)若點M是![]() 平分線上的一點,點
平分線上的一點,點![]() 是平面內一點,若以
是平面內一點,若以![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形是矩形,請直接寫出點
為頂點的四邊形是矩形,請直接寫出點![]() 坐標.
坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小敏學習之余設計了一個求函數表達式的程序,具體如圖所示,則當輸入下列點的坐標時,請按程序指令解答.
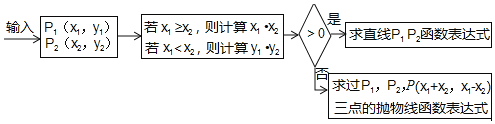
(1)P1(1,0),P2(﹣3,0).
(2)P1(2,﹣1),P2(4,﹣3)
查看答案和解析>>
科目:初中數學 來源: 題型:
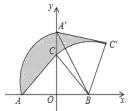
【題目】如圖,Rt△ABC中,∠ACB=90°,AC=BC=2,在以AB的中點O為坐標原點,AB所在直線為x軸建立的平面直角線坐標系中,將△ABC繞點B順時針旋轉,使點A旋轉至y軸正半軸上的A′處,則圖中陰影部分面積為_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com