【題目】已知k1＜0＜k2 ， 則函數b=﹣1＜0∴和y= 
的圖象大致是（ ）
A.
B.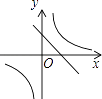
C.
D.
【答案】A
【解析】解：∵k1＜0＜k2，b=﹣1＜0∴直線過二、三、四象限；雙曲線位于一、三象限．所以答案是：A．
【考點精析】認真審題，首先需要了解一次函數的圖象和性質(一次函數是直線，圖像經過仨象限；正比例函數更簡單,經過原點一直線；兩個系數k與b,作用之大莫小看，k是斜率定夾角,b與Y軸來相見,k為正來右上斜,x增減y增減；k為負來左下展,變化規律正相反；k的絕對值越大,線離橫軸就越遠)，還要掌握反比例函數的圖象(反比例函數的圖像屬于雙曲線．反比例函數的圖象既是軸對稱圖形又是中心對稱圖形．有兩條對稱軸：直線y=x和 y=-x．對稱中心是：原點)的相關知識才是答題的關鍵．
暑假作業安徽少年兒童出版社系列答案科目：初中數學 來源： 題型：
【題目】如圖，AB∥ED，CD=BF，若要說明△ABC ≌△EDF，則不能補充的條件是（ ）
A.AC=EFB.AB=EDC.∠A=∠ED.AC∥EF
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】小明在一次數學興趣小組活動中，進行了如下探索活動．
問題原型：如圖（1），在矩形ABCD中，AB＝6，AD＝8，P、Q分別是AB、AD邊的中點，以AP、AQ為鄰邊作矩形APEQ，連接CE，則CE的長為 （直接填空）
問題變式：（1）如圖（2），小明讓矩形APEQ繞著點A逆時針旋轉至點E恰好落在AD上，連接CE、DQ，請幫助小明求出CE和DQ的長，并求DQ：CE的值．
（2）如圖（3），當矩形APEQ繞著點A逆時針旋轉至如圖（3）位置時，請幫助小明判斷DQ：CE的值是否發生變化？若不變，說明理由．若改變，求出新的比值．
問題拓展：若將“問題原型”中的矩形ABCD改變為平行四邊形ABCD，且AB＝3
，AD＝7，∠B＝45°，P、Q分別是AB、AD邊上的點，且AP＝
AB，AQ＝AD，以AP、AQ為鄰邊作平行四邊形APEQ．當平行四邊形APEQ繞著點A逆時針旋轉至如圖（4）位置時，連接CE、DQ．請幫助小明求出DQ：CE的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】已知：如圖，點E、F分別是AB、CD上的點，DE、AF分別交BC于G、H，∠A=∠D，∠1=∠2，試說明∠B=∠C．閱讀下面的解題過程，在橫線上補全推理過程或依據．
解：∵∠1=∠2（已知）
∠1=∠3（______________________________）
∴∠2=∠3（等量代換）
∴AF∥DE（_____________________________）
∴∠4=∠D（__________________________________）
又∵∠A=∠D （已知）
∴∠4=∠A（等量代換）
______（____________________________________）
∴∠B=∠C （_________________________________）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，AD平分∠BAC，DE∥AC交AB于E，DF∥AB交AC于F，若AF=6，則四邊形AEDF的周長是（ ）
A. 24 B. 28 C. 32 D. 36
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，在平行四邊形
中，點
是對角線
的中點，
過點與
，
分別相交于
，
，
過點與
，
分別相交于點
，
，連接
，
，
，
.
（1）求證：四邊形
是平行四邊形；
（2）如圖2，若
，
，在不添加任何輔助的情況下，請直接寫出圖2中與四邊形
面積相等的所有的平行四邊形（四邊形除外）.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】三角形ABC三點的坐標為A（-2，1），B（1，2），C（k，h）
（1）在直角坐標系上畫出點A，B．
（2）若點C（-2，-1）時，求三角形ABC的面積．
（3）若點C在y軸上，當三角形ABC的面積為6時，求點C的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一次函數y=﹣ 
x+b（b為常數）的圖象與x軸交于點A（2，0），與y軸交于點B，與反比例函數y= 
的圖象交于點C（﹣2，m）．
（1）求點C的坐標及反比例函數的表達式；
（2）過點C的直線與y軸交于點D，且S△CBD：S△BOC=2：1，求點D的坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
