
【題目】如圖,拋物線y=ax2+bx+c的圖象,經(jīng)過(guò)點(diǎn)A(1,0),B(3,0),C(0,3)三點(diǎn),過(guò)點(diǎn)C,D(﹣3,0)的直線與拋物線的另一交點(diǎn)為E.
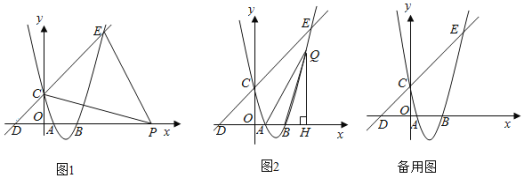
(1)請(qǐng)你直接寫出:
①拋物線的解析式 ;
②直線CD的解析式 ;
③點(diǎn)E的坐標(biāo)( , );
(2)如圖1,若點(diǎn)P是x軸上一動(dòng)點(diǎn),連接PC,PE,則當(dāng)點(diǎn)P位于何處時(shí),可使得∠CPE=45°,請(qǐng)你求出此時(shí)點(diǎn)P的坐標(biāo);
(3)如圖2,若點(diǎn)Q是拋物線上一動(dòng)點(diǎn),作QH⊥x軸于H,連接QA,QB,當(dāng)QB平分∠AQH時(shí),請(qǐng)你直接寫出此時(shí)點(diǎn)Q的坐標(biāo).
【答案】(1)①y=x2﹣4x+3,②y=x+3,③(5,8);(2)P1(1,0),P2(9,0);(3)Q(3+![]() ,3+2
,3+2![]() ).
).
【解析】
(1)①假設(shè)拋物線的解析式為y=a(x﹣1)(x﹣3),將A,B代入,即可求出拋物線的解析式;
②設(shè)直線CD的解析式為y=kx+b,將C,D代入可得直線CD的解析式;
③聯(lián)立兩個(gè)解析式可得E點(diǎn)坐標(biāo);
(2)過(guò)點(diǎn)E作EH⊥x軸于H,由已知可推出CD=![]() ,DE=
,DE=![]() ,EC=
,EC=![]() ,△ECP∽△EPD,由此可得PE2,根據(jù)勾股定理可得PH,由此即可求出點(diǎn)P的坐標(biāo);
,△ECP∽△EPD,由此可得PE2,根據(jù)勾股定理可得PH,由此即可求出點(diǎn)P的坐標(biāo);
(3)延長(zhǎng)QH到M,使得HM=1,連接AM,BM,延長(zhǎng)QB交AM于N,設(shè)Q(t,t2﹣4t+3),由題意得點(diǎn)Q只能在點(diǎn)B的右側(cè)的拋物線上,則QH=t2﹣4t+3,BH=t﹣3,AH=t﹣1,由此可推出△QHB∽△AHM,據(jù)此可得QN⊥AM,當(dāng)BM=AB=2時(shí),QN垂直平分線段AM,此時(shí)QB平分∠AQH,根據(jù)勾股定理可得t值,即可推出點(diǎn)Q坐標(biāo).
(1)①∵拋物線經(jīng)過(guò)A(1,0),B(3,0),
∴可以假設(shè)拋物線的解析式為y=a(x﹣1)(x﹣3),
把C(0,3)代入得到a=1,
∴拋物線的解析式為y=x2﹣4x+3;
②設(shè)直線CD的解析式為y=kx+b,則有![]() ,
,
解得![]() ,
,
∴直線CD的解析式為y=x+3;
③由![]() ,解得
,解得![]() 或
或![]() ,
,
∴E(5,8),
故答案為:y=x2﹣4x+3,y=x+3,(5,8);
(2)如圖1中,過(guò)點(diǎn)E作EH⊥x軸于H,
∵C(0,3),D(﹣3,0),E(5,8),
∴OC=OD=3,EH=8,
∴∠PDE=45°,CD=![]() ,DE=
,DE=![]() ,EC=
,EC=![]() ,
,
當(dāng)∠CPE=45°時(shí),∵∠PDE=∠EPC,∠CEP=∠PED,
∴△ECP∽△EPD,
∴![]() ,
,
∴PE2=ECED=80,
在Rt△EHP中,PH=![]() =
=![]() =4,
=4,
∴把點(diǎn)H向左或向右平移4個(gè)單位得到點(diǎn)P,
∴P1(1,0),P2(9,0);
(3)延長(zhǎng)QH到M,使得HM=1,連接AM,BM,延長(zhǎng)QB交AM于N,

設(shè)Q(t,t2﹣4t+3),由題意得點(diǎn)Q只能在點(diǎn)B的右側(cè)的拋物線上,則QH=t2﹣4t+3,BH=t﹣3,AH=t﹣1,
∴![]() =
=![]() =t﹣3=
=t﹣3=![]() ,
,
∵∠QHB=∠AHM=90°,
∴△QHB∽△AHM,
∴∠BQH=∠HAM,
∵∠BQH+∠QBH=90°,∠QBH=∠ABN,
∴∠HAM+∠ABN=90°,
∴∠ANB=90°,
∴QN⊥AM,
∴當(dāng)BM=AB=2時(shí),QN垂直平分線段AM,此時(shí)QB平分∠AQH,
在Rt△BHM中,BH=![]() =
=![]() =
=![]() ,
,
∴t=3+![]() ,
,
∴Q(3+![]() ,3+2
,3+2![]() ).
).



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著疫情的有效控制我省百大項(xiàng)目之一的哈爾濱地鐵“二號(hào)線三號(hào)線”全面復(fù)工修建,建設(shè)方通過(guò)合理化地施工設(shè)計(jì),加大適當(dāng)?shù)耐度雭?lái)彌補(bǔ)前期耽誤的工作量,以保證今年修建目標(biāo)的實(shí)現(xiàn)。修建過(guò)程中有大量的殘土需要運(yùn)輸。某車隊(duì)有載重量為8噸、10噸的卡車共12輛,全部車輛運(yùn)輸一次可以運(yùn)輸110噸殘土.
(1)求該車隊(duì)有載重量為8噸、10噸的卡車各多少輛?
(2)隨著工程的進(jìn)展,該車隊(duì)需要一次運(yùn)輸殘土不低于165噸,為了完成任務(wù),該車隊(duì)準(zhǔn)備新購(gòu)進(jìn)這兩種卡車共6輛,則最多購(gòu)進(jìn)載重量為8噸的卡車多少輛?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
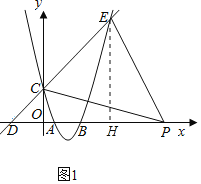
【題目】如圖,已知雙曲線y=![]() 和直線y=-x+2,P是雙曲線第一象限上一動(dòng)點(diǎn),過(guò)P作y軸的平行線,交直線y=-x+2于Q點(diǎn),O為坐標(biāo)原點(diǎn).
和直線y=-x+2,P是雙曲線第一象限上一動(dòng)點(diǎn),過(guò)P作y軸的平行線,交直線y=-x+2于Q點(diǎn),O為坐標(biāo)原點(diǎn).

(1)求直線y=-x+2與坐標(biāo)軸圍成三角形的周長(zhǎng);
(2)設(shè)△PQO的面積為S,求S的最小值.
(3)設(shè)定點(diǎn)R(2,2),以點(diǎn)P為圓心,PR為半徑畫⊙P,設(shè)⊙P與直線y=-x+2交于M、N兩點(diǎn).
①判斷點(diǎn)Q與⊙P的位置關(guān)系,并說(shuō)明理由;
②求S△MON=S△PMN時(shí)的P點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知關(guān)于x的一元二次方程x2+(2m+1)x+m2﹣2=0.
(1)若該方程有兩個(gè)實(shí)數(shù)根,求m的最小整數(shù)值;
(2)若方程的兩個(gè)實(shí)數(shù)根為x1,x2,且(x1﹣x2)2+m2=21,求m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,已知A(0,6),B(2,0),C(6,0),D為線段BC上的動(dòng)點(diǎn),以AD為邊向右側(cè)作正方形ADEF,連接CF交DE于點(diǎn)P,則CP的最大值_____.
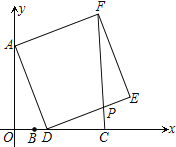
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
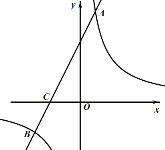
【題目】如圖,在平面直角坐標(biāo)系中,一次函數(shù)![]() (
(![]() ≠
≠![]() )的圖象與反比例函數(shù)
)的圖象與反比例函數(shù)![]() (
(![]() )的圖象交于A、B兩點(diǎn),與
)的圖象交于A、B兩點(diǎn),與![]() 軸交于C點(diǎn),點(diǎn)A的坐標(biāo)為(
軸交于C點(diǎn),點(diǎn)A的坐標(biāo)為(![]() ,6),點(diǎn)C的坐標(biāo)為(-2,0),且
,6),點(diǎn)C的坐標(biāo)為(-2,0),且![]() .
.
(1)求該反比例函數(shù)和一次函數(shù)的解析式;
(2)求點(diǎn)B的坐標(biāo);
(3)利用圖象求不等式:![]() .
.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】四張撲克牌的點(diǎn)數(shù)分別是2,5,6,8,除點(diǎn)數(shù)不同外,其余都相同,將它們洗勻后背面朝上放在桌上
(1)若從中隨機(jī)抽取一張牌,則抽出的牌的點(diǎn)數(shù)是偶數(shù)的概率為 ;
(2)若隨機(jī)抽取一張牌不放回,接著再抽取一張牌,請(qǐng)用列表法或畫樹狀圖法(只選其中一種)表示出所有可能出現(xiàn)的結(jié)果,并求所抽兩張牌的點(diǎn)數(shù)都是偶數(shù)的概率.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在平面直角坐標(biāo)系xOy中,點(diǎn)A的坐標(biāo)為A(1,0),等腰直角三角形ABC的邊AB在x軸的正半軸上,∠ABC=90°,點(diǎn)B在點(diǎn)A的右側(cè),點(diǎn)C在第一象限.將△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)75°,如果點(diǎn)C的對(duì)應(yīng)點(diǎn)E恰好落在y軸的正半軸上,那么點(diǎn)C的坐標(biāo)為_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】我們知道求函數(shù)圖象的交點(diǎn)坐標(biāo),可以聯(lián)立兩個(gè)函數(shù)解析式組成方程組,方程組的解就是交點(diǎn)的坐標(biāo).如:求直線y=2x+3與y=﹣x+6的交點(diǎn)坐標(biāo),我們可以聯(lián)立兩個(gè)解析式得到方程組![]() ,解得
,解得![]() ,所以直線y=2x+3與y=﹣x+6的交點(diǎn)坐標(biāo)為(1,5).請(qǐng)利用上述知識(shí)解決下列問題:
,所以直線y=2x+3與y=﹣x+6的交點(diǎn)坐標(biāo)為(1,5).請(qǐng)利用上述知識(shí)解決下列問題:
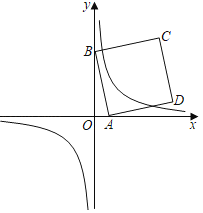
(1)已知直線y=kx﹣2和拋物線y=x2﹣2x+3,
①當(dāng)k=4時(shí),求直線與拋物線的交點(diǎn)坐標(biāo);
②當(dāng)k為何值時(shí),直線與拋物線只有一個(gè)交點(diǎn)?
(2)已知點(diǎn)A(a,0)是x軸上的動(dòng)點(diǎn),B(0,4![]() ),以AB為邊在AB右側(cè)做正方形ABCD,當(dāng)正方形ABCD的邊與反比例函數(shù)y=
),以AB為邊在AB右側(cè)做正方形ABCD,當(dāng)正方形ABCD的邊與反比例函數(shù)y=![]() 的圖象有4個(gè)交點(diǎn)時(shí),試求a的取值范圍.
的圖象有4個(gè)交點(diǎn)時(shí),試求a的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com