
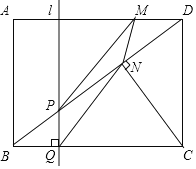
【題目】如圖,在矩形ABCD中,CD=3cm,BC=4cm,連接BD,并過點C作CN⊥BD,垂足為N,直線l垂直BC,分別交BD、BC于點P、Q.直線l從AB出發,以每秒1cm的速度沿BC方向勻速運動到CD為止;點M沿線段DA以每秒1cm的速度由點D向點A勻速運動,到點A為止,直線1與點M同時出發,設運動時間為t秒(t>0).
(1)線段CN= ;
(2)連接PM和QN,當四邊形MPQN為平行四邊形時,求t的值;
(3)在整個運動過程中,當t為何值時△PMN的面積取得最大值,最大值是多少?
【答案】(1)![]() ;(2)t=
;(2)t=![]() ;(3)t=4時,△PMN的面積取得最大值,最大值為
;(3)t=4時,△PMN的面積取得最大值,最大值為![]() .
.
【解析】
(1)由矩形的性質和勾股定理可求BD的長,由三角形的面積公式可求CN的長;
(2)由勾股定理可求DN的長,通過證明△DMN∽△DAB,可得![]() ,可得DM的值,即可求t的值;
,可得DM的值,即可求t的值;
(3)分兩種情況討論,利用三角形面積公式列出△PMN的面積與t的關系式,可求△PMN的面積的最大值.
解:(1)∵四邊形ABCD是矩形
∴BC=AD=4cm,∠BCD=90°=∠A,
∴BD=![]() =5cm,
=5cm,
∵S△BCD=![]() BC
BC![]() CD=
CD=![]() BD
BD![]() CN
CN
∴CN=![]()
故答案為:![]()
(2)在Rt△CDN中,DN=![]() =
=![]()
∵四邊形MPQN為平行四邊形時
∴PQ∥MN,且PQ⊥BC,AD∥BC
∴MN⊥AD
∴MN∥AB
∴△DMN∽△DAB
∴![]()
即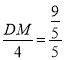
∴DM=![]() cm
cm
∴t=![]()
(3)∵BD=5,DN=![]()
∴BN=![]()
如圖,過點M作MH⊥BD于點H,
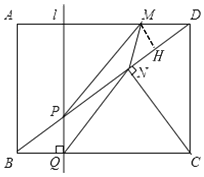
∵sin∠MDH=sin∠BDA=![]()
∴![]()
∴MH=![]() t
t
當0<t<![]()
∵BQ=t,
∴BP=![]() t,
t,
∴PN=BD﹣BP﹣DN=5﹣![]() ﹣
﹣![]() t=
t=![]() ﹣
﹣![]() t
t
∴S△PMN=![]() ×PN×MH=
×PN×MH=![]() ×
×![]() t×(
t×(![]() ﹣
﹣![]() t)=﹣
t)=﹣![]() t2+
t2+![]() t
t
∴當t=![]() s時,S△PMN有最大值,且最大值為
s時,S△PMN有最大值,且最大值為![]() ,
,
當t=![]() s時,點P與點N重合,點P,點N,點M不構成三角形;
s時,點P與點N重合,點P,點N,點M不構成三角形;
當![]() <t≤4時,如圖,
<t≤4時,如圖,
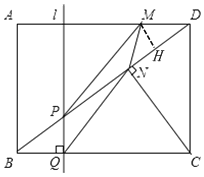
∴PN=BP﹣BN=![]() t﹣
t﹣![]()
∴S△PMN=![]() ×PN×MH=
×PN×MH=![]() ×
×![]() t×(
t×(![]() t﹣
t﹣![]() )=
)=![]() t2﹣
t2﹣![]() t
t
當![]() <t≤4時,S△PMN隨t的增大而增大,
<t≤4時,S△PMN隨t的增大而增大,
∴當t=4時,S△PMN最大值為![]() ,
,
∵![]() >
>![]()
∴綜上所述:t=4時,△PMN的面積取得最大值,最大值為![]() .
.


 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,函數![]() 的圖象G經過點
的圖象G經過點![]() ,直線
,直線![]() 與y軸交于點B,與圖象G交于點C.
與y軸交于點B,與圖象G交于點C.
(1)求m的值.
(2)橫、縱坐標都是整數的點叫做整點.記圖象G在點A,C之間的部分與線段BA,BC圍成的區域(不含邊界)為W.
①當直線l過點![]() 時,直接寫出區域W內的整點個數.
時,直接寫出區域W內的整點個數.
②若區域W內的整點不少于4個,結合函數圖象,求k的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某超市促銷活動,將A,B,C三種水果采用甲、乙、丙三種方式搭配裝進禮盒進行銷售.每盒的總成本為盒中A,B,C三種水果成本之和,盒子成本忽略不計.甲種方式每盒分別裝A,B,C三種水果6kg,3kg,1kg;乙種方式每盒分別裝A,B,C三種水果2kg,6kg,2kg.甲每盒的總成本是每千克A水果成本的12.5倍,每盒甲的銷售利潤率為20%;每盒甲比每盒乙的售價低25%;每盒丙在成本上提高40%標價后打八折出售,獲利為每千克A水果成本的1.2倍.當銷售甲、乙、丙三種方式搭配的禮盒數量之比為2:2:5時,則銷售總利潤率為_____.(利潤率=利潤÷成本×100%)
查看答案和解析>>
科目:初中數學 來源: 題型:
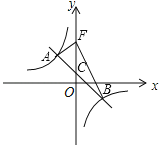
【題目】在平面直角坐標系中,一次函數y=﹣x+b的圖象與反比例函數y=![]() (k≠0)的圖象交于A、B點,與y軸交于點C,其中點A的半標為(﹣2,3)
(k≠0)的圖象交于A、B點,與y軸交于點C,其中點A的半標為(﹣2,3)
(1)求一次函數和反比例函數的解析式;
(2)如圖,若將點C沿y軸向上平移4個單位長度至點F,連接AF、BF,求△ABF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,AB=8.
(1)作△ABC的內角∠CAB的平分線,與邊BC交于點D(用尺規作圖,保留作圖痕跡,不要求寫作法);
(2)若AD=BD,求CD的長度.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水產品養殖企業為指導該企業某種產品的養殖和銷售,對歷年市場行情和水產品的養殖情況進行了調查.調查發現這種水產品的每千克售價![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足關系式
(月)滿足關系式![]() +36,而其每千克成本
+36,而其每千克成本![]() (元)與銷售月份
(元)與銷售月份![]() (月)滿足的函數關系如圖所示:
(月)滿足的函數關系如圖所示:
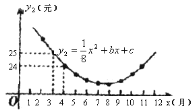
(1)試確定![]() 、
、![]() 的值;
的值;
(2)求出這種水產品每千克的利潤![]() (元)與銷售月份
(元)與銷售月份![]() (月)之間的函數關系式;
(月)之間的函數關系式;
(3)幾月份出售這種水產品每千克利潤最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“雙11”當天,重慶順風快遞公司出動所有車輛分上午、下午兩批往成都送件,該公司共有甲、乙、丙三種車型,其中甲型車數量占公司車輛總數的![]() ,乙型車輛是丙型車數量的2倍,上午安排甲車數量的
,乙型車輛是丙型車數量的2倍,上午安排甲車數量的![]() ,乙車數量的
,乙車數量的![]() ,丙車數量的
,丙車數量的![]() 進行運輸,且上午甲、乙、丙三種車型每輛載貨量分別為15噸,10噸,20噸,則上午剛好運完當天全部快件重量的
進行運輸,且上午甲、乙、丙三種車型每輛載貨量分別為15噸,10噸,20噸,則上午剛好運完當天全部快件重量的![]() ;下午安排剩下的所有車輛運輸完當天剩下的所有快件,且下午甲、乙、丙三種車型每輛載貨量分別不得超過20噸,12噸,16噸,下午乙型車實際載貨量為下午甲型車每輛實際載貨量的
;下午安排剩下的所有車輛運輸完當天剩下的所有快件,且下午甲、乙、丙三種車型每輛載貨量分別不得超過20噸,12噸,16噸,下午乙型車實際載貨量為下午甲型車每輛實際載貨量的![]() .已知同種貨車每輛的實際載貨量相等,甲、乙、丙三種車型每輛車下午的運輸成本分別為50元/噸,90元/噸,60元/噸.則下午運輸時,一輛甲種車、一輛乙種車、一輛丙種車總的運輸成本最少為_____元.
.已知同種貨車每輛的實際載貨量相等,甲、乙、丙三種車型每輛車下午的運輸成本分別為50元/噸,90元/噸,60元/噸.則下午運輸時,一輛甲種車、一輛乙種車、一輛丙種車總的運輸成本最少為_____元.
查看答案和解析>>
科目:初中數學 來源: 題型:
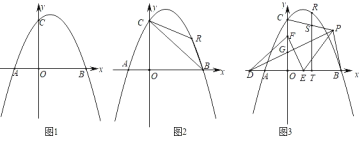
【題目】已知:在平面直角坐標系中,拋物線y=ax2﹣2ax+4(a<0)交x軸于點A、B,與y軸交于點C,AB=6.
(1)如圖1,求拋物線的解析式;
(2)如圖2,點R為第一象限的拋物線上一點,分別連接RB、RC,設△RBC的面積為s,點R的橫坐標為t,求s與t的函數關系式;
(3)在(2)的條件下,如圖3,點D在x軸的負半軸上,點F在y軸的正半軸上,點E為OB上一點,點P為第一象限內一點,連接PD、EF,PD交OC于點G,DG=EF,PD⊥EF,連接PE,∠PEF=2∠PDE,連接PB、PC,過點R作RT⊥OB于點T,交PC于點S,若點P在BT的垂直平分線上,OB﹣TS=![]() ,求點R的坐標.
,求點R的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校開展了以“不忘初心,牢記使命”為主題的知識競賽,現從該校八、九年級各隨機抽取10名學生的成績進行整理,描述和分析(成績用m表示),共分成四個組:A.80≤m<85,B.85≤m<90,C.90≤m<95,D.95≤m≤100.另外給出了部分信息如下:
八年級10名學生的成績:99,80,99,86,99,96,90,100,89,82.
九年級10名學生的成績在C組的數據:94,90,94.
八、九年級抽取學生成績統計表 | ||
年級 | 八年級 | 九年級 |
平均數 | 92 | 92 |
中位數 | 93 | b |
眾數 | c | 100 |
方差 | 52 | 50.4 |
根據以上信息,解答下列問題:
(1)上面圖表中的a= ,b= ,c= .
(2)扇形統計圖中“D組”所對應的圓心角的度數為 .
(3)根據以上信息,你認為哪個年級的學生對“不忘初心,牢記使命”的內容掌握較好?說明理由.(一條即可)
(4)該校九年級共有840名學生參加了知識競賽活動,估計九年級參加此次知識競賽活動成績為較好(90≤m<95)的學生有多少人?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com