
【題目】某公司計劃從甲、乙兩種產品中選擇一種生產并銷售,每年產銷x件.已知產銷兩種產品的有關信息如表:
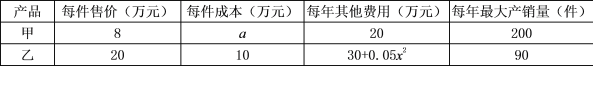
其中a為常數,且5≤a≤7.
(1)若產銷甲、乙兩種產品的年利潤分別為![]() 萬元、
萬元、![]() 萬元,直接寫出
萬元,直接寫出![]() 、
、![]() 與x的函數關系式;(注:年利潤=總售價﹣總成本﹣每年其他費用)
與x的函數關系式;(注:年利潤=總售價﹣總成本﹣每年其他費用)
(2)分別求出產銷兩種產品的最大年利潤;
(3)為獲得最大年利潤,該公司應該選擇產銷哪種產品?請說明理由.
【答案】(1)1)y1=(8-a)x-20,(0<x≤200),![]() =
=![]() (0<x≤90);(2)x=200時,y1的值最大=(1580-200a)萬元,當x=90時,
(0<x≤90);(2)x=200時,y1的值最大=(1580-200a)萬元,當x=90時,![]() 最大值=465萬元;(3)答案見解析
最大值=465萬元;(3)答案見解析
【解析】
(1)根據利潤=銷售數量×每件的利潤即可解決問題.
(2)根據一次函數的增減性,二次函數的增減性即可解決問題.
(3)根據題意分三種情形分別求解即可:①(1580-200a)=465,②(1580-200a)>465,③(1580-200a)<465.
(1) 解:(1)y1=(8-a)x-20,(0<x≤200)
![]() =
=![]() .(0<x≤90).
.(0<x≤90).
(2)對于y1=(8-a)x-20.
∵8-a>0,∴x=200時,y1的值最大=(1580-200a)萬元.
對于![]() .
.
∵0<x≤90,∴x=90時,![]() 最大值=465萬元.
最大值=465萬元.
(3)①(1580-200a)=465,解得a=5.575,②(1580-200a)>465,解得a<5.575,③(1580-200a)<465,解得a>5.575.
∵5≤a≤7,∴當a=5.575時,生產甲乙兩種產品的利潤相同.
當5≤a<5.575時,生產甲產品利潤比較高.
當5.575<a≤7時,生產乙產品利潤比較高.
(每種情況1分)


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】密碼鎖有三個轉輪,每個轉輪上有十個數字:0,1,2,…9.小黃同學是9月份中旬出生,用生日“月份+日期”設置密碼:9×× (注:中旬為某月中的11日-20日),小張同學要破解其密碼:
(1)第一個轉輪設置的數字是9,第二個轉輪設置的數字可能是幾.
(2)請你幫小張同學列舉出所有可能的密碼,并求密碼數能被3整除的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
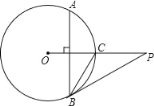
【題目】如圖,已知P是⊙O外一點,PO交⊙O于點C,OC=CP=4,弦AB⊥OC,劣弧AB的度數為120°,連接PB.
(1)求BC的長;
(2)求證:PB是⊙O的切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知△ABC三個頂點的坐標分別是A(2,2),B(4,0),C(4,﹣4).
(1)請在圖中,畫出△ABC向左平移6個單位長度后得到的△A1B1C1;
(2)以點O為位似中心,將△ABC縮小為原來的![]() ,得到△A2B2C2,請在圖中y軸右側,畫出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,請在圖中y軸右側,畫出△A2B2C2,并求出∠A2C2B2的正弦值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某學校開展“青少年科技創新比賽”活動,“喜洋洋”代表隊設計了一個遙控車沿直線軌道AC做勻速直線運動的模型.甲、乙兩車同時分別從A,B出發,沿軌道到達C處,在AC上,甲的速度是乙的速度的1.5倍,設t分后甲、乙兩遙控車與B處的距離分別為d1,d2(單位:米),則d1,d2與t的函數關系如圖,試根據圖象解決下列問題.

(1)填空:乙的速度v2=________米/分;
(2)寫出d1與t的函數表達式;
(3)若甲、乙兩遙控車的距離超過10米時信號不會產生相互干擾,試探究什么時間兩遙控車的信號不會產生相互干擾?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】三張背面完全相同的卡片,它們的正面分別標有數字﹣1,0,1,將他們背面朝上,洗勻后隨機抽取一張,把正面的數字作為b,接著再抽取一張,把正面的數字作為c,則滿足關于x的一元二次方程x2+bx+c=0有實數根的概率是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知二次函數y=ax2+bx+3 的圖象與x軸分別交于A(1,0),B(3,0)兩點,與y軸交于點C
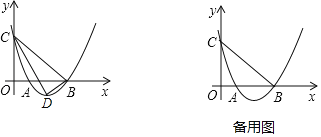
(1)求此二次函數解析式;
(2)點D為拋物線的頂點,試判斷△BCD的形狀,并說明理由;
(3)將直線BC向上平移t(t>0)個單位,平移后的直線與拋物線交于M,N兩點(點M在y軸的右側),當△AMN為直角三角形時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)己知,如圖1,△ABC是⊙O的內接正三角形,點P為弧BC上一動點,請探究PA,PB,PC三者之間有何數量關系,并給予證明.
(2)如圖2,四邊形ABCD是⊙O的內接正方形,點P為弧BC上一動點,請探究PA,PB,PC三者之間有何數量關系,并給予證明.
(3)如圖3,六邊形ABCDEF是⊙O的內接正六邊形,點P為弧BC上一動點,請探究PA、PB、PC三者之間有何數量關系,直接寫出結論不需證明.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com