
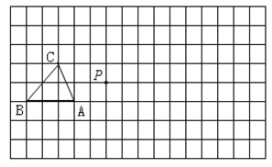
【題目】在下面的正方形網格中,每個小正方形的邊長為1個單位,△ABC是格點三角形(頂點在網格交點處) .
(1)作出△ABC的中心對稱圖形△![]() ,A點為對稱中心;
,A點為對稱中心;
(2)作出△ABC關于點P的位似△A'B'C',且位似比為1:2;
(3)在圖中畫出以A、B、C為頂點的平行四邊形的第四個頂點D.
【答案】(1)見解析; (2) 見解析;(3)見解析
【解析】
(1)由A為對稱中心,故A點不動,連接BA并延長,使![]() ,連接CA并延長,使
,連接CA并延長,使![]() ,連接
,連接![]() ,
,![]() 為
為![]() 關于A中心對稱的圖形,如圖所示;
關于A中心對稱的圖形,如圖所示;
(2)連接AP并延長,使A′P=2AP,連接BP并延長,使B′P=2BP,連接CP并延長,使C′P=2CP,連接A′B′,A′C′,B′C′,△A′B′C′為所求作的三角形;
(3)滿足題意的D點有3個,分別是以AB為對角線作出的平行四邊形ACBD1,以AC為對角線的平行四邊形ABCD2,以BC為對角線的平行四邊形ABD3C,如圖所示.
(1)如圖所示:![]() 為所求作的三角形;
為所求作的三角形;

(2)如圖所示:△A′B′C′為所求作的三角形;
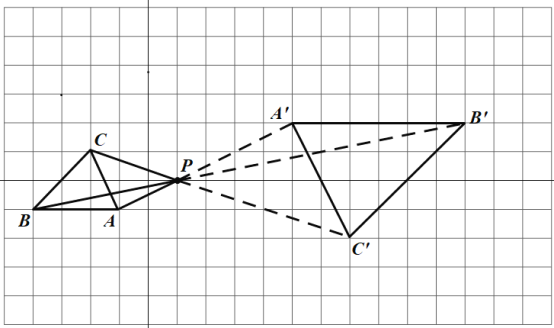
(3)如圖所示:D1,D2,D3為所求作的點.



科目:初中數學 來源: 題型:
【題目】某校九年級為了解學生課堂發言情況,隨機抽取該年級部分學生,對他們某天在課堂上發言的次數進行了統計,其結果如表,并繪制了如圖所示的兩幅不完整的統計圖,已知B、E兩組發言人數的比為5:2,請結合圖中相關數據回答下列問題:
(1)則樣本容量是 ,并補全直方圖;
(2)該年級共有學生500人,請估計全年級在這天里發言次數不少于12的次數;
(3)已知A組發言的學生中恰有1位女生,E組發言的學生中有2位男生,現從A組與E組中分別抽一位學生寫報告,請用列表法或畫樹狀圖的方法,求所抽的兩位學生恰好是一男一女的概率.
發言次數n | |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的部分圖象如圖所示,圖象過點
的部分圖象如圖所示,圖象過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,下列結論:
,下列結論:![]() ;
;![]() >0;(3)若點
>0;(3)若點![]() 、點
、點![]() 、點
、點![]() 在該函數圖象上,則
在該函數圖象上,則![]() ;
;![]() 若方程
若方程![]() 的兩根為
的兩根為![]() 和
和![]() ,且
,且![]() ,則
,則![]() 其中正確的結論是______.
其中正確的結論是______.
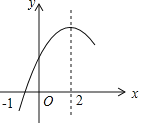
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,CB=CA,∠ACB=90°,點D在邊BC上(與B,C不重合),四邊形ADEF為正方形,過點F作FG⊥CA,交CA的延長線于點G,連接FB,交DE于點Q,給出以下結論:①AC=FG;②S△FAB∶S四邊形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正確結論的個數是( )

A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD邊長為4,M、N分別是BC、CD上的兩個動點,當M點在BC上運動時,保持AM和MN垂直,

(1)證明:Rt△ABM ∽Rt△MCN;
(2)設BM=x,梯形ABCN的面積為y,求y與x之間的函數關系式;當M點運動到什么位置時,四邊形ABCN的面積最大,并求出最大面積;
(3)當M點運動到什么位置時Rt△ABM∽Rt△AMN,求此時x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線![]() 與
與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,拋物線
,拋物線![]() 經過點
經過點![]() ,
,![]() .
.

(1)求點B的坐標和拋物線的解析式;
(2)M(m,0)為x軸上一個動點,過點M垂直于x軸的直線與直線AB和拋物線分別交于點P、N,
①點![]() 在線段
在線段![]() 上運動,若以
上運動,若以![]() ,
,![]() ,
,![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,求點
相似,求點![]() 的坐標;
的坐標;
②點![]() 在
在![]() 軸上自由運動,若三個點
軸上自由運動,若三個點![]() ,
,![]() ,
,![]() 中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱
中恰有一點是其它兩點所連線段的中點(三點重合除外),則稱![]() ,
,![]() ,
,![]() 三點為“共諧點”.請直接寫出使得
三點為“共諧點”.請直接寫出使得![]() ,
,![]() ,
,![]() 三點成為“共諧點”的
三點成為“共諧點”的![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
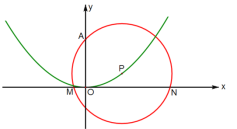
【題目】如圖,拋物線y=ax2+bx+c(a、b、c是常數,a≠0)經過原點O和![]() 兩點,點P在該拋物線上運動,以點P為圓心的⊙P總經過定點A(0, 2).
兩點,點P在該拋物線上運動,以點P為圓心的⊙P總經過定點A(0, 2).
(1)a= ,b= ,c= ;
(2)求證:在點P運動的過程中,⊙P始終與x軸相交;
(3)設⊙P與x軸相交于M、N兩點,M在N的左邊.當△AMN為等腰三角形時,直接寫出圓心P的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】像![]() =x這樣的方程,可以通過方程兩邊平方把它轉化為2x+3=x2,解得x1=3,x2=﹣1.但由于兩邊平方,可能產生增根,所以需要檢驗,經檢驗,當x1=3時,
=x這樣的方程,可以通過方程兩邊平方把它轉化為2x+3=x2,解得x1=3,x2=﹣1.但由于兩邊平方,可能產生增根,所以需要檢驗,經檢驗,當x1=3時,![]() =3滿足題意;當x2=﹣1時,
=3滿足題意;當x2=﹣1時,![]() =﹣1不符合題意;所以原方程的解是x=3.運用以上經驗,則方程x+
=﹣1不符合題意;所以原方程的解是x=3.運用以上經驗,則方程x+![]() =1的解為_____.
=1的解為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:![]() 和
和![]() 都是等邊三角形,點
都是等邊三角形,點![]() 在邊
在邊![]() 上,連接
上,連接![]() .
.
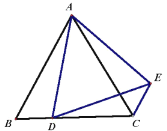
(1)如圖1,求證:![]() ;
;
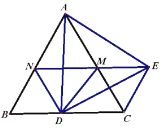
(2)如圖2,點![]() 在
在![]() 上,
上,![]() (
(![]() ),連接
),連接![]() 并延長交
并延長交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,在不添加任何輔助線的情況下,請直接寫出圖2中所有與線段
,在不添加任何輔助線的情況下,請直接寫出圖2中所有與線段![]() 相等的線段(線段
相等的線段(線段![]() 除外).
除外).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com