
【題目】如圖,在四邊形ABCD中,![]() ,AE交BC于點P,交DC的延長線于點E,點P為AE的中點.
,AE交BC于點P,交DC的延長線于點E,點P為AE的中點.
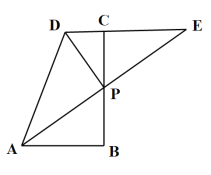
(1)求證:點P也是BC的中點.
(2)若![]() ,且
,且![]() ,求AP的長.
,求AP的長.
(3)在(2)的條件下,若線段AE上有一點Q,使得![]() 是等腰三角形,求
是等腰三角形,求![]() 的長.
的長.
【答案】(1)證明見詳解;(2)5;(3)4或![]() 或
或![]() .
.
【解析】
(1)由![]() ,得∠B=∠ECP,由點P為AE的中點,得AP=EP,根據AAS可證CEPBAP,進而得到結論;
,得∠B=∠ECP,由點P為AE的中點,得AP=EP,根據AAS可證CEPBAP,進而得到結論;
(2)在RtDCP中,利用勾股定理,可得CP的長,即BP的長,從而在RtABP中,利用勾股定理,即可求解;
(3)若![]() 是等腰三角形,分3種情況討論:①當AQ=AB時,②當BQ=AB時,③當AQ=BQ時,分別根據等腰三角形的性質和勾股定理求出AQ的值即可.
是等腰三角形,分3種情況討論:①當AQ=AB時,②當BQ=AB時,③當AQ=BQ時,分別根據等腰三角形的性質和勾股定理求出AQ的值即可.
(1)∵![]() ,
,
∴∠B=∠ECP,
∵點P為AE的中點,
∴AP=EP,
在CEP和BAP中,
∵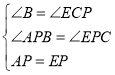 (對頂角相等)
(對頂角相等)
∴CEPBAP(AAS)
∴BP=CP,
∴點P也是BC的中點;
(2)∵![]() ,
,![]()
∴![]() ,
,
∴![]()
![]() ,
,
∴BP=CP=3,
∴在RtABP中,![]()
(3)若![]() 是等腰三角形,分3種情況討論:
是等腰三角形,分3種情況討論:
①當AQ=AB時,如圖1,
∵AB=4,
∴AQ=4;
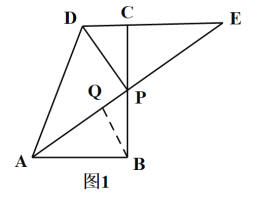
②當BQ=AB時,如圖2,

過段B作BM⊥AE于點M,
∵在RtABP中,AB=4,BP=3,AP=5,
∴BM=![]() ,
,
∵在RtABM中,![]() ,
,
∴![]() ,
,
∵BQ=AB,BM⊥AE,
∴MQ=AM=![]() ,
,
∴AQ=2×![]() =
=![]() ,
,
③當AQ=BQ時,
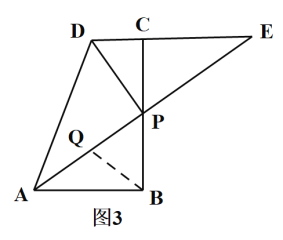
∴∠QAB=∠QBA,
∵![]() ,
,
∴∠QAB+∠QPB=90°,∠QBA+∠QBP=90°,
∴∠QPB=∠QBP,
∴BQ=PQ,
∴AQ= BQ=PQ=![]() AP=
AP=![]() ×5=
×5=![]() ;
;
綜上所述,AQ的長為:4或![]() 或
或![]() .
.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
【題目】2018中國重慶開州漢豐湖國際摩托艇公開賽第二年舉辦.鄰近區縣一旅行社去年組團觀看比賽,全團共花費9600元.今年賽事宣傳工作得力,該旅行社繼續組團前來觀看比賽,人數比去年增加了![]() ,總費用增加了3900元,人均費用反而下降了20元.
,總費用增加了3900元,人均費用反而下降了20元.
(1)求該旅行社今年有多少人前來觀看賽事?
(2)今年該旅行社本次費用中,其它費用不低于交通費的2倍,求人均交通費最多為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,下列結論:①abc>0;②2a+b>0;③b2﹣4ac>0;④a﹣b+c>0,其中正確的個數是( )
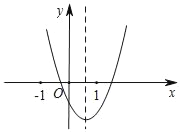
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:(一)如果我們能找到兩個實數x、y使![]() 且
且![]() ,這樣
,這樣![]() ,那么我們就稱
,那么我們就稱![]() 為“和諧二次根式”,則上述過程就稱之為化簡“和諧二次根式”.
為“和諧二次根式”,則上述過程就稱之為化簡“和諧二次根式”.
例如:![]() .
.
(二)在進行二次根式的化簡與運算時,我們有時還會碰上如![]() 一樣的式子,其實我們還可以將其進一步化簡:
一樣的式子,其實我們還可以將其進一步化簡: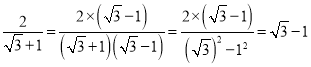 ,那么我們稱這個過程為分式的分母有理化.
,那么我們稱這個過程為分式的分母有理化.
根據閱讀材料解決下列問題:
(1)化簡“和諧二次根式”:①![]() ___________,②___________;
___________,②___________;
(2)已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)設![]() 的小數部分為
的小數部分為![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數![]() 的圖象經過點
的圖象經過點![]() .
.
(1)若函數圖象經過原點,求k,b的值
(2)若點![]() 是該函數圖象上的點,當
是該函數圖象上的點,當![]() 時,總有
時,總有![]() ,且圖象不經過第三象限,求k的取值范圍.
,且圖象不經過第三象限,求k的取值范圍.
(3)點![]() 在函數圖象上,若
在函數圖象上,若![]() ,求n的取值范圍.
,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知:關于x的二次函數![]() 的圖象與x軸交于點A(1,0)和點B,與y軸交于點C(0,3),拋物線的對稱軸與x軸交于點D.
的圖象與x軸交于點A(1,0)和點B,與y軸交于點C(0,3),拋物線的對稱軸與x軸交于點D.
(1)求二次函數的表達式;
(2)在y軸上是否存在一點P,使△PBC為等腰三角形.若存在,請求出點P的坐標;
(3)有一個點M從點A出發,以每秒1個單位的速度在AB上向點B運動,另一個點N從點D與點M同時出發,以每秒2個單位的速度在拋物線的對稱軸上運動,當點M到 達點B時,點M、N同時停止運動,問點M、N運動到何處時,△MNB面積最大,試求出最大面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點C在AB上,![]() 、
、![]() 均是等邊三角形,
均是等邊三角形,![]() 、
、![]() 分別與
分別與![]() 交于點
交于點![]() ,則下列結論:①
,則下列結論:①![]() ;②
;②![]() ;③
;③![]() 為等邊三角形;④
為等邊三角形;④![]() ∥
∥![]() ;⑤DC=DN正確的有( )個
;⑤DC=DN正確的有( )個
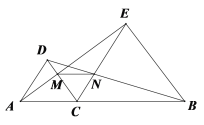
A.2個B.3個C.4個D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com