
【題目】如圖,拋物線 ![]() 與
與 ![]() 軸交于
軸交于![]() 和
和![]() ,與
,與 ![]() 軸交于
軸交于 ![]() 點,點
點,點![]() 關于拋物線的對稱軸的對稱點為點
關于拋物線的對稱軸的對稱點為點![]() .
.
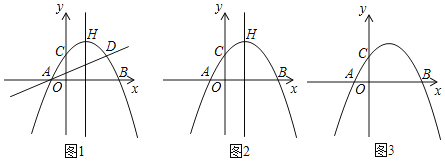
(1)求此拋物線的解析式和對稱軸.
(2)如圖 2,當點![]() 在拋物線的對稱軸上運動時,在直線
在拋物線的對稱軸上運動時,在直線![]() 上是否存在點
上是否存在點![]() ,使得以點
,使得以點![]() 、
、![]() 、
、![]() 、
、![]() 為頂點的四邊形為平行四邊形?若存在,請求出點
為頂點的四邊形為平行四邊形?若存在,請求出點 ![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(3)如圖 3,當點![]() 、
、![]() 、
、![]() 三點共圓時,請求出該圓圓心的坐標.
三點共圓時,請求出該圓圓心的坐標.
【答案】(1)![]() ,x=1;(2)存在,點 F 的坐標為
,x=1;(2)存在,點 F 的坐標為![]() 或
或![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)把點 ![]() 和
和![]() 代入
代入 ![]() 中求出解析式,再求出對稱軸即可;
中求出解析式,再求出對稱軸即可;
(2)分分三種情況討論,作出示意圖,求出點F的坐標即可;
(3)分別作 ![]() 的垂直平分線,它們的交點為
的垂直平分線,它們的交點為 ![]() 點,
點,![]() 點就是點
點就是點 ![]() 、
、![]() 、
、![]() 三點共圓的圓心,先表示出EF和FM,再根據
三點共圓的圓心,先表示出EF和FM,再根據![]() 求出即可.
求出即可.
解:(1)把點 ![]() 和
和![]() 代入
代入 ![]() ,得
,得
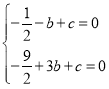
解得:![]() ,
,
∴拋物線的解析式為:![]() ,
,
∴對稱軸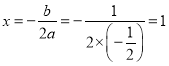 ;
;
(2)存在,分三種情況討論,
①如圖 1 所示,
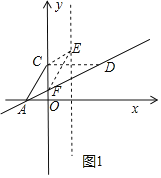
∵四邊形![]() 為平行四邊形,
為平行四邊形,
∴![]() 可由
可由![]() 平移得到,點
平移得到,點![]() 的對應點為點
的對應點為點![]() ,點
,點![]() 的對應點為點
的對應點為點 ![]() ,
,
∵![]() ,點
,點 ![]() 的橫坐標為 1,
的橫坐標為 1,
∴向右平移了一個單位,
∵![]() ,
,
∴點![]() 的橫坐標為 0,
的橫坐標為 0,
設直線 ![]() 的函數解析式為:
的函數解析式為: ![]() ,
,
把點![]() 和
和 ![]() 代入,得
代入,得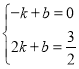 ,
,
解得:![]() ,
,
∴直線![]() 的函數解析式為:
的函數解析式為:![]() ,
,
∴當![]() 時,
時, ![]() ,
,
∴![]() ;
;
②如圖 2 所示,
此時點![]() 與點
與點 ![]() 重合,
重合,
![]() ;
;
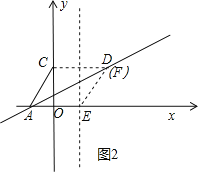
③如圖 3 所示,

根據平移的規律,得知點 ![]() 的橫坐標為﹣2,
的橫坐標為﹣2,
當 ![]() 時,
時,![]() ,
,
![]() ;
;
綜上所述:點 F 的坐標為![]() 或
或![]() 或
或![]() ;
;
(3)如圖,分別作 ![]() 的垂直平分線,它們的交點為
的垂直平分線,它們的交點為 ![]() 點,
點,![]() 點就是點
點就是點 ![]() 、
、![]() 、
、![]() 三點共圓的圓心,
三點共圓的圓心,
∵點![]() 是
是 ![]() 的中點,
的中點,
![]() ,
,
設直線 ![]() 的解析式為:
的解析式為: ![]() ,
,
把 ![]() 代入上式,得
代入上式,得![]() ,
,
![]() ,
,
當 ![]() 時,
時,![]() ,解得:
,解得:![]() ,
,
,
當![]() 時,
時,![]() ,
,
![]() ,
,
如圖,易證得:![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
當![]() 時,
時,![]() ,,
,,
∴點 ![]() 、
、![]() 、
、![]() 三點共線的圓的圓心坐標為
三點共線的圓的圓心坐標為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,AB=4cm,動點E從點A出發,以1cm/秒的速度沿折線AB—BC的路徑運動,到點C停止運動.過點E作 EF∥BD,EF與邊AD(或邊CD)交于點F,EF的長度y(cm)與點E的運動時間x(秒)的函數圖象大致是

A. 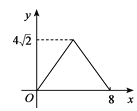 B.
B. 
C. 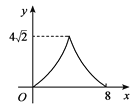 D.
D. 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:求1+2+22+23+24+…+22017的值.
解:設S=1+2+22+23+24+…+22017,
將等式兩邊同時乘以2得,2S=2+22+23+24+25+…+22017+22018,
將下式減去上式得:2S-S=22018-1,即S=22018-1,
所以1+2+22+23+24+…+2201722018-1,
請你依照此法計算:
(1)1+2+22+23+24+…+29;
(2)1+5+52+53+54+…+5n(其中n為正整數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正六邊形ABCDEF的邊長為![]() ,點G,H,I,J,K,L依次在正六邊形的六條邊上,且AG=BH=CI=DJ=EK=FL,順次連結G,I,K,和H,J,L,則圖中陰影部分的周長C的取值范圍為( )
,點G,H,I,J,K,L依次在正六邊形的六條邊上,且AG=BH=CI=DJ=EK=FL,順次連結G,I,K,和H,J,L,則圖中陰影部分的周長C的取值范圍為( )
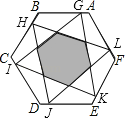
A.6≤C≤6![]() B.3≤C≤3
B.3≤C≤3![]() C.3
C.3![]() ≤C≤6D.3
≤C≤6D.3![]() ≤C≤6
≤C≤6![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知平面直角坐標系中,點C(3,4),以OC為邊作菱形OABC,且點A落在x軸的正半軸上,點D為y軸上的一個動點,設D(0,m),連結DB,交直線OC于點E.
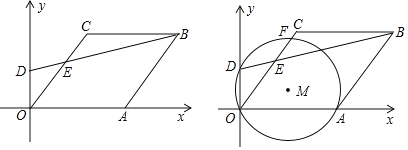
(1)填空:B的坐標為( ),sin∠AOC= ;
(2)當點D在y軸正半軸時,記△DEO的面積為S1,△BCE的面積為S2,當S1=S2時,求m的值.
(3)過點D,O,A作⊙M,交線段OC于點F.
①當⊙M與菱形OABC一邊所在的直線相切時,求所有滿足條件的m的值.
②當OD=DE時,直接寫出OE:EF的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:平行四邊形ABCD的兩邊AB,AD的長是關于x的方程x2﹣mx+![]() ﹣
﹣![]() =0的兩個實數根.
=0的兩個實數根.
(1)m為何值時,四邊形ABCD是菱形?求出這時菱形的邊長;
(2)若AB的長為2,那么ABCD的周長是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
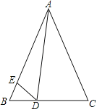
【題目】如圖,在△ABC中,AB=AC,點D、E分別在BC、AB上,且∠BDE=∠CAD.
(1)求證:△BDE∽△CAD;
(2)求證:△ADE∽△ABD.
查看答案和解析>>
科目:初中數學 來源: 題型:
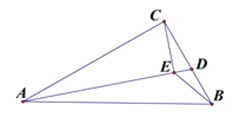
【題目】如圖,在△ABC中,AB=13cm,AC=12cm,BC=5cm.D是BC邊上的一個動點,連接AD,過點C作CE⊥AD于E,連接BE,在點D變化的過程中,線段BE的最小值是( )
A.2.5B.![]()
![]() C.
C.![]() D.5
D.5
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com