
【題目】在平面直角坐標系![]() 中,已知二次函數
中,已知二次函數![]() 的圖象與x軸交于點
的圖象與x軸交于點![]() ,與y軸交于點B,將其圖象在點A,B之間的部分(含A,B兩點)記為F.
,與y軸交于點B,將其圖象在點A,B之間的部分(含A,B兩點)記為F.
(1)求點B的坐標及該函數的表達式;
(2)若二次函數![]() 的圖象與F只有一個公共點,結合函數圖象,求a的取值范圍.
的圖象與F只有一個公共點,結合函數圖象,求a的取值范圍.
【答案】(1)點B的坐標為![]() .
. ![]() . (2)
. (2)![]() 或
或![]() .
.
【解析】
(1)令x=0可求出y的值,從而得到點B的坐標;把點A坐標代入![]() 求出m的值即可得到結論;
求出m的值即可得到結論;
(2)畫出函數圖象,再利用圖象確定a的取值范圍即可.
(1)∵![]() 的圖象與y軸交于點B,
的圖象與y軸交于點B,
∴點B的坐標為![]() .
.
∵![]() 的圖象與x軸交于點
的圖象與x軸交于點![]() ,
,
∴將![]() 代入
代入![]() 可得
可得![]() .
.
∴![]() .
.
∴該函數的表達式為![]() .
.
(2)∵將二次函數![]() 的圖象在點A,B之間的部分(含A,B兩點)記為F,
的圖象在點A,B之間的部分(含A,B兩點)記為F,
∴F的端點為A,B,并經過拋物線![]() 的頂點C(其中C點坐標為
的頂點C(其中C點坐標為![]() ).
).
∴可畫F如圖1所示.
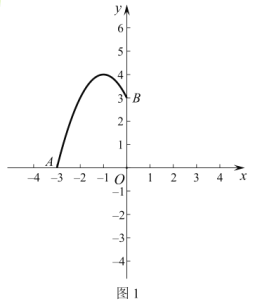
∵二次函數![]() 的圖象的對稱軸為
的圖象的對稱軸為![]() ,且與F只有一個公共點,
,且與F只有一個公共點,
∴可分別把A,B,C的坐標代入解析式![]() 中.
中.
∴可得三個a值分別為![]() ,3,5.
,3,5.
畫示意圖如圖2所示.
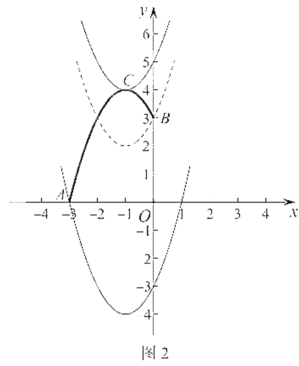
∴結合函數圖象可知:
二次函數![]() 的圖象與F只有一個公共點時,a的取值范圍是
的圖象與F只有一個公共點時,a的取值范圍是![]() 或
或![]() .
.


科目:初中數學 來源: 題型:
【題目】大家知道烏鴉喝水的故事,如圖,它看到一個水位較低的瓶子,喝不著水,沉思一會后聰明的烏鴉銜來一個個小石子放入瓶中,水位上升后,烏鴉喝到了水.從烏鴉看到瓶子的那刻起開始計時,設時間變量為![]() ,水位高度變量為
,水位高度變量為![]() ,下列圖象中最符合故事情景的大致圖象是( )
,下列圖象中最符合故事情景的大致圖象是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C、D為圓上的兩點,OC∥BD,弦AD與BC,OC分別交于E、F
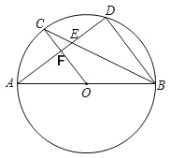
(1)求證:![]() =
=![]() ;
;![]()
(2)若CE=1,EB=3,求⊙O的半徑;
(3)若BD=6,AB=10,求D E的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小元設計的“過直線外一點作已知直線的平行線”的尺規作圖過程.

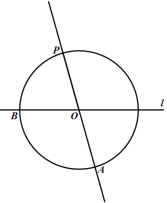
已知:如圖,直線l和直線外一點P.
求作:過點P作直線l的平行線.
作法:如圖,
①在直線l上任取點O;
②作直線![]() ;
;
③以點O為圓心![]() 長為半徑畫圓,交直線
長為半徑畫圓,交直線![]() 于點A,交直線l于點B;
于點A,交直線l于點B;
④連接![]() ,以點B為圓心,
,以點B為圓心,![]() 長為半徑畫弧,交
長為半徑畫弧,交![]() 于點C(點A與C不重合);
于點C(點A與C不重合);
⑤作直線![]() .
.
則直線![]() 即為所求.
即為所求.
根據小元設計的尺規作圖過程,完成以下任務.
(1)補全圖形;
(2)完成下面的證明:
證明:連接![]()
∵![]()
∴![]()
∴![]() _______
_______![]() _________,
_________,
又∵![]() ,
,
∴![]() _______
_______![]() _________,
_________,
∴![]() ,
,
∴![]() (___________________________)(填推理的依據).
(___________________________)(填推理的依據).
查看答案和解析>>
科目:初中數學 來源: 題型:
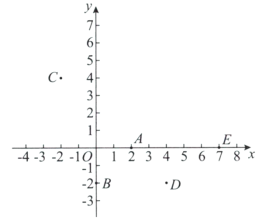
【題目】如圖,在平面直角坐標系![]() 中,有五個點
中,有五個點![]() ,將二次函數
,將二次函數![]() 的圖象記為W.下列的判斷中
的圖象記為W.下列的判斷中
①點A一定不在W上;
②點B,C,D可以同時在W上;
③點C,E不可能同時在W上.
所有正確結論的序號是_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
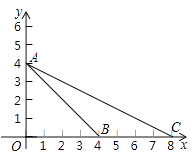
【題目】如圖,在平面直角坐標系xOy中,點A,B,C的坐標分別是(0,4),(4,0),(8,0),⊙M是△ABC的外接圓,則點M的坐標為___________.
查看答案和解析>>
科目:初中數學 來源: 題型:
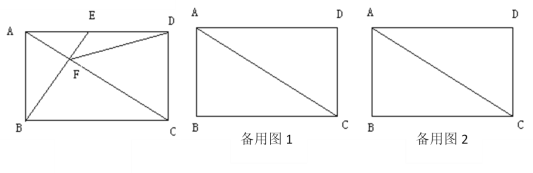
【題目】如圖,在矩形ABCD中,AB=3,BC=4,點E在AD上,BE與AC交于點F.
(1)若AC⊥BE,求AE的長 ;
(2)設△DEF和△DCF的面積分別為S1和S2,當AE=m時,求S1:S2;
(3)當AE的長是多少時,△DCF是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人在一條長為600m的筆直道路上均勻地跑步,速度分別為![]() 和
和![]() ,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
,起跑前乙在起點,甲在乙前面50m處,若兩人同時起跑,則從起跑出發到其中一人先到達終點的過程中,兩人之間的距離y(m)與時間t(s)的函數圖象是( )
A.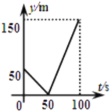 B.
B.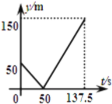 C.
C.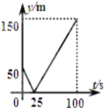 D.
D.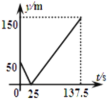
查看答案和解析>>
科目:初中數學 來源: 題型:
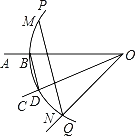
【題目】如圖:已知銳角∠AOC,依次按照以下順序操作畫圖:
(1)在射線OA上取一點B,以點O為圓心,OB長為半徑作![]() ,交射線OC于點D,連接BD;
,交射線OC于點D,連接BD;
(2)分別以點B,D為圓心,BD長為半徑作弧,交![]() 于點M,N;
于點M,N;
(3)連接ON,MN.
根據以上作圖過程及所作圖形可知下列結論:①OC平分∠AON;②MN∥BD;③MN=3BD;④若∠AOC=30°,則MN=![]() ON.其中正確結論的序號是_____.
ON.其中正確結論的序號是_____.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com