
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,

(1)圖1中共有_______對相似三角形;
(2)已知![]() ,請求出
,請求出![]() 的長;
的長;
(3)在(2)的情況下,如果以![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,點
軸,點![]() 為坐標原點
為坐標原點![]() ,建立直角坐標系(如圖2),若點
,建立直角坐標系(如圖2),若點![]() 從
從![]() 點出發,以每秒1個單位的速度沿線段
點出發,以每秒1個單位的速度沿線段![]() 運動,點
運動,點![]() 出
出![]() 點出發,以每秒1個單位的速度沿線段BA運動,其中一點最先到達線段的端點時,兩點即刻同時停止運動:設運動時間為
點出發,以每秒1個單位的速度沿線段BA運動,其中一點最先到達線段的端點時,兩點即刻同時停止運動:設運動時間為![]() 秒是否存在點
秒是否存在點![]() ,使以點
,使以點![]() 為頂點的三角形與
為頂點的三角形與![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(1)3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;(2)4.8;(3)點P的坐標為(1.35,3)或(3.15,1.8).
【解析】
(1)根據直角三角形性質和相似三角形判定可得結果;(2)根據勾股定理和三角形面積公式可得;(3)分類討論:①當∠BQP=90°時,如圖2①,此時△PQB∽△ACB;②當∠BPQ=90°時,如圖2②,此時△QPB∽△ACB;根據相似三角形性質和勾股定理可得.
(1)根據已知可得:∠A=∠BCD, ∠B=∠ACD,故:圖1中共有3對相似三角形,分別為:△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD.
故答案為3,△ABC∽△ACD,△ABC∽△CBD,△ABC∽△CBD;
(2)如圖1,在△ABC中,∵∠ACB=90°,AB=10,AC=8,
∴BC=![]() =6.
=6.
∵△ABC的面積=![]() ABCD=
ABCD=![]() ACBC,
ACBC,
∴CD=![]() =4.8;
=4.8;
(3)存在點P,使以點B、P、Q為頂點的三角形與△ABC相似,理由如下:
在△BOC中,∵∠COB=90°,BC=6,OC=4.8,
∴OB=![]() =3.6.
=3.6.
分兩種情況:
①當∠BQP=90°時,如圖2①,此時△PQB∽△ACB,
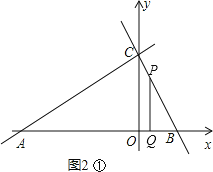
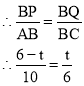
解得t=2.25,即BQ=CP=2.25,
∴OQ=OB-BQ=3.6-2.25=1.35,BP=BC-CP=6-2.25=3.75.
在△BPQ中,由勾股定理,得PQ=![]() =
=![]() =3,
=3,
∴點P的坐標為(1.35,3);
②當∠BPQ=90°時,如圖2②,此時△QPB∽△ACB,
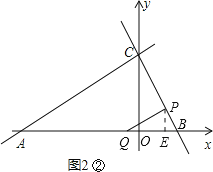
∴![]()
![]() ∴
∴![]() ,
,
解得t=3.75,即BQ=CP=3.75,BP=BC-CP=6-3.75=2.25.
過點P作PE⊥x軸于點E.
∵△QPB∽△ACB,
∴![]() ,即
,即![]() ,
,
∴PE=1.8.
在△BPE中,BE=![]() =0.45,
=0.45,
∴OE=OB-BE=3.6-0.45=3.15,
∴點P的坐標為(3.15,1.8);
綜上可得,點P的坐標為(1.35,3)或(3.15,1.8).


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,點D從點C出發沿CA方向以4cm/s的速度向點A勻速運動,同時點E從點A出發沿AB方向以2cm/s的速度向點B勻速運動,當其中一個點到達終點時,另一個點也隨之停止運動.設點D、E運動的時間是ts.過點D作DF⊥BC于點F,連接DE、EF.

(1)用t的代數式表示:AE= ;DF= ;
(2)四邊形AEFD能夠成為菱形嗎?如果能,求出相應的t值;如果不能,請說明理由;
(3)當t為何值時,△DEF為直角三角形?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司生產一種節能型燈具并加以銷售,現準備在甲市和乙市按不同的方案進行銷售,若只在甲市銷售,銷售價為![]() (元/件),月銷售量為
(元/件),月銷售量為![]() (件),
(件),![]() 是
是![]() 的一次函數.如表所示,成本為50元/件,無論銷售多少,每月還需支出廣告費用72500元。設月利潤為
的一次函數.如表所示,成本為50元/件,無論銷售多少,每月還需支出廣告費用72500元。設月利潤為![]() (元),(利潤=銷售額-成本-廣告費).若只在乙市銷售,銷售價為200元/件,受各種因素影響,成本為
(元),(利潤=銷售額-成本-廣告費).若只在乙市銷售,銷售價為200元/件,受各種因素影響,成本為![]() 元/件(
元/件(![]() 為常數且
為常數且![]() ),當月銷售量為
),當月銷售量為![]() 件時,每月還需交納
件時,每月還需交納![]() 的附加費,設月利潤為
的附加費,設月利潤為![]() (元).(利潤=銷售額-成本-附加費)
(元).(利潤=銷售額-成本-附加費)
月銷售量 | 1500 | 2000 |
銷售價格 | 185 | 180 |
(1)當![]() 時,
時,![]() ______元/件,
______元/件,![]() ______元(直接寫出結果).
______元(直接寫出結果).
(2)分別求出![]() 、
、![]() 與
與![]() 的函數關系式(不必寫出
的函數關系式(不必寫出![]() 的取值范圍).
的取值范圍).
(3)當![]() 為何值時,
為何值時,![]() 最大?若在乙市銷售月利潤最大值與甲市最大值相同,求
最大?若在乙市銷售月利潤最大值與甲市最大值相同,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,⊙O是△ABC外接圓,點D是圓上一點,點D、B分別在AC兩側,且BD=BC,連接AD、BD、OD、CD,延長CB到點P,使∠APB=∠DCB.
(1)求證:AP為⊙O的切線;
(2)若⊙O的半徑為1,當△OED是直角三角形時,求△ABC的面積;
(3)若△BOE、△DOE、△AED的面積分別為a、b、c,試探究a、b、c之間的等量關系式,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
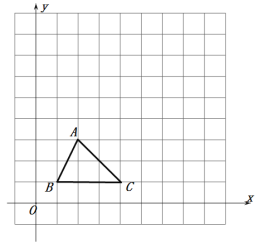
【題目】如圖,在邊長為1的小正方形網格中:
(1)![]() 向上平移6個單位長度,再向右平移5個單位長度后得到
向上平移6個單位長度,再向右平移5個單位長度后得到![]() ,則
,則![]() 的坐標為______;
的坐標為______;
(2)以點![]() 為位似中心,將
為位似中心,將![]() 放大為原來的2倍,得到
放大為原來的2倍,得到![]() ,請在網格中畫出
,請在網格中畫出![]() .
.
(3)![]() 的周長為_________________,面積為_________________.
的周長為_________________,面積為_________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正比例函數y1=x的圖象與反比例函數![]() (k≠0)的圖象相交于A、B兩點,點A的縱坐標為2.
(k≠0)的圖象相交于A、B兩點,點A的縱坐標為2.
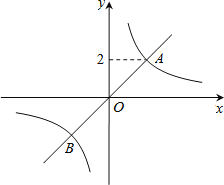
(1)求反比例函數的解析式;
(2)求出點B的坐標,并根據函數圖象,寫出當y1>y2時,自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,用長為6m的鋁合金條制成“日”字形窗框,若窗框的寬為xm,窗戶的透光面積為ym2(鋁合金條的寬度不計).
(1)求出y與x的函數關系式;
(2)如何安排窗框的長和寬,才能使得窗戶的透光面積最大?并求出此時的最大面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
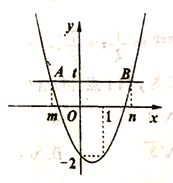
【題目】如圖為二次函數![]() 圖象,直線
圖象,直線![]() 與拋物線交于
與拋物線交于![]() 兩點,
兩點,![]() 兩點橫坐標分別為
兩點橫坐標分別為![]() 根據函數圖象信息有下列結論:
根據函數圖象信息有下列結論:
①![]() ;
;
②若對于![]() 的任意值都有
的任意值都有![]() ,則
,則![]() ;
;
③![]() ;
;
④![]() ;
;
⑤當![]() 為定值時若
為定值時若![]() 變大,則線段
變大,則線段![]() 變長
變長
其中,正確的結論有__________(寫出所有正確結論的番號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com