【題目】如圖，把矩形ABCD沿EF翻折，點B恰好落在AD邊的B′處，若AE=2，DE=6，∠EFB=60°，則矩形ABCD的面積是（ ）
A. 12B. 24C. 12
D. 16
【答案】D
【解析】
在矩形ABCD中根據AD∥BC得出∠DEF=∠EFB=60°，由折疊的性質可得∠A=∠A′=90°，A′E=AE=2，AB=A′B′，∠A′EF=∠AEF=180°-60°=120°，∠A′EB′=60°．根據直角三角形的性質得出A′B′=AB=2
，然后根據矩形的面積公式列式計算即可得解．
在矩形ABCD中，
∵AD∥BC，
∴∠B′EF=∠EFB=60°，
由折疊的性質得∠A=∠A′=90°，A′E=AE=2，AB=A′B′，∠A′EF=∠AEF=180°-60°=120°，
∴∠A′EB′=∠A′EF-∠B′EF=120°-60°=60°．
在Rt△A′EB′中，
∵∠A′B′E=90°-60°=30°，
∴B′E=2A′E，而A′E=2，
∴B′E=4，
∴A′B′=2，即AB=2，
∵AE=2，DE=6，
∴AD=AE+DE=2+6=8，
∴矩形ABCD的面積=ABAD=2×8=16．
故選：D．
科目：初中數學 來源： 題型：
【題目】同樣大小的黑色棋子按圖中所示的規律擺放：
（1）填寫下表：
圖形序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | … |
圖中棋子數 | 6 | 9 |
|
|
|
|
| … |
（2）照這樣的方式擺下去，寫出擺第n（n為正整數）個圖形所需黑色棋子的顆數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】甲三角形的周長為
，乙三角形的第一條邊長為
，第二條邊長為
，第三條邊比第二條邊短
．
（1）求乙三角形第三條邊的長；
（2）甲、乙兩三角形的周長哪個大？試說明理由；
（3）a、b都為正整數，甲、乙兩三角形的周長在數軸上表示的點分別為A、B，若A、B兩點之間恰好有18個“整數點”（點表示的數為整數），求a的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，AB是⊙O的直徑，BD是⊙O的弦，延長BD到點C，使DC=BD，連結AC，過點D作DE⊥AC，垂足為E．
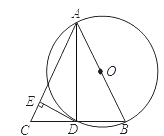
（1）求證：AB=AC；
（2）求證：DE為⊙O的切線；
（3）若⊙O半徑為5，∠BAC=60°，求DE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
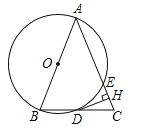
【題目】如圖，在△ABC中，AB=AC，以AB為直徑的⊙O與邊BC，AC分別交于D，E兩點，過點D作DH⊥AC于點H．
（1）判斷DH與⊙O的位置關系，并說明理由；
（2）求證：H為CE的中點；
（3）若BC=10，cosC=
，求AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，4張如圖1的長為a，寬為b（a＞b）長方形紙片，按圖2的方式放置，陰影部分的面積為S1，空白部分的面積為S2，若S2＝2S1，則a，b滿足（ ）
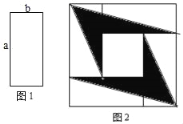
A. a＝
B. a＝2bC. a＝
bD. a＝3b
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】水果種植大戶小芳，為了吸引更多的顧客，組織了觀光采摘游活動，每一位來采摘水果的顧客都有一次抽獎機會，在一只不透明的盒子里有A（蘋果），B（梨子），C（葡萄），D（葡萄）四張外形完全相同的卡片，抽獎時先隨機抽取一張卡片，再從盒子中剩下的3張中隨機抽取第二張．
（1）請利用樹狀圖或列表的方法，表示前后兩次抽得的卡片所有可能的情況；
（2）如果抽得的兩張卡片是同一種水果圖片就可獲得獎勵，那么得到獎勵的概率是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC中，點O是邊AC上一個動點，過O作直線MN∥BC．設MN交∠ACB的平分線于點E，交∠ACB的外角平分線于點F．
（1）求證：OE=OF；
（2）若CE=12，CF=5，求OC的長；
（3）當點O在邊AC上運動到什么位置時，四邊形AECF是矩形？并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了宣傳2018年世界杯，實現“足球進校園”的目標，任城區某中學計劃為學校足球隊購買一批足球，已知購買2個A品牌的足球和3個B品牌的足球共需380元；購買4個A品牌的足球和2個B品牌的足球共需360元．
（1）求A，B兩種品牌的足球的單價．
（2）學校準備購進這兩種品牌的足球共50個，并且B品牌足球的數量不少于A品牌足球數量的4倍，請設計出最省錢的購買方案，求該方案所需費用，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com