
【題目】如圖,等邊三角形![]() 的邊長為
的邊長為![]() ,且其三個頂點均在拋物線
,且其三個頂點均在拋物線![]() 上.
上.
(1)求拋物線的解析式;
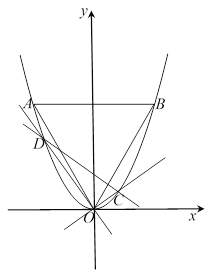
(2)若過原點![]() 的直線
的直線![]() 與直線
與直線![]() 分別交拋物線
分別交拋物線![]() 于點
于點![]() 、
、![]() ,
,
①當![]() 時,試求
時,試求![]() 的面積;
的面積;
②試證明:不論實數![]() 取何值,直線
取何值,直線![]() 總是經過一定點.
總是經過一定點.
【答案】(1)![]() ;(2)①20;②詳見解析
;(2)①20;②詳見解析
【解析】
(1)如圖,由題意可得OB=![]() ,∠ABO=60°,然后在Rt△BOF中,利用解直角三角形的知識求出BF和OF的長,進而可得點B坐標,然后代入拋物線的解析式即可求出結果;
,∠ABO=60°,然后在Rt△BOF中,利用解直角三角形的知識求出BF和OF的長,進而可得點B坐標,然后代入拋物線的解析式即可求出結果;
(2)①先解方程組求出點C、D的坐標,再利用待定系數法求出直線CD的解析式,然后即可求出直線![]() 與
與![]() 軸的交點
軸的交點![]() ,再根據
,再根據![]() 計算即可;
計算即可;
②先解方程組求出點C、D的坐標,再利用待定系數法求出直線CD的解析式,然后即可求出直線![]() 與
與![]() 軸的交點,進而可得結論.
軸的交點,進而可得結論.
解:(1)如圖,![]() 等邊△
等邊△![]() 的邊長為
的邊長為![]() ,
,
∴OB=![]() ,∠ABO=60°,
,∠ABO=60°,
則在Rt△BOF中,BF=4,![]() ,
,
![]() ,
,
又點![]() 在拋物線
在拋物線![]() 上,
上,
![]()
![]() ,解得:
,解得:![]() ,
,
故所求的解析式為![]() ;
;
(2)①解方程組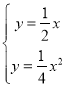 ,得
,得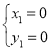 ,
,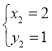 ,∴
,∴![]() ,
,
解方程組 ,得
,得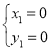 ,
, ,∴
,∴![]() ,
,
設直線![]() 的解析式為
的解析式為![]() ,
,
![]() ,解得:
,解得: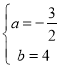 ,
,
所以直線![]() 的解析式為
的解析式為![]() ,
,
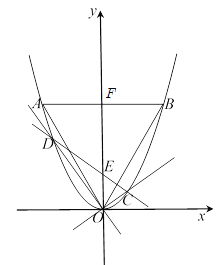
設直線![]() 與
與![]() 軸交于點
軸交于點![]() ,則
,則![]() ,如圖,
,如圖,

∵![]() ,
,![]() ,
,
![]() ;
;
②解方程組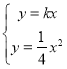 ,得
,得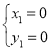 ,
,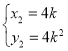 ,∴
,∴![]() ,
,
解方程組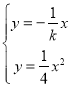 ,得
,得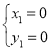 ,
,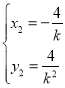 ,∴
,∴![]() ,
,
設直線![]() 解析式為
解析式為![]() ,
,
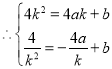 ,解得:
,解得: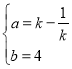 ,
,
所以直線![]() 的解析式為
的解析式為![]() ,
,
所以不論實數![]() 取何值,直線
取何值,直線![]() 總過定點
總過定點![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,將正方形![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后得到正方形
后得到正方形![]() ,依此方式,繞點
,依此方式,繞點![]() 連續旋轉
連續旋轉![]() 次得到正方
次得到正方![]() ,如果點
,如果點![]() 的坐標為
的坐標為![]() ,那么
,那么![]() 的坐標為( )
的坐標為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB//CD,直線EF交AB于點E,交CD于點F,EP平分∠AEF,FP平分∠CFE,∠BEP=α,∠DFP=β,則a+β=( )

A.180°B.225°C.270°D.315°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,投擲一枚均勻的硬幣,落地時正面或反面向上的可能性相同.有甲、乙兩人做投硬幣實驗,他們分別投硬幣100次,結果“正面向上”的次數為:甲60次、乙40次.
(1)求甲、乙做投硬幣實驗“正面向上”的頻率各是多少?
(2)若甲、乙同時做第101次投硬幣實驗,求“正面都向上”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
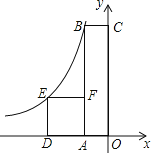
【題目】如圖,四邊形OABC是矩形,四邊形ADEF是正方形,點A、D在x軸的負半軸上,點C在y軸的正半軸上,點F在AB上,點B、E在反比例函數y=![]() (k為常數,k≠0)的圖象上,正方形ADEF的面積為4,且BF=2AF,則k值為_____.
(k為常數,k≠0)的圖象上,正方形ADEF的面積為4,且BF=2AF,則k值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一張矩形ABCD紙片中,AD=30,AB=25,先將這張紙片沿著過點A的直線折疊,使得點B落在矩形的對稱軸上,折痕交矩形的邊于點E,則折痕AE的長為_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為![]() 的正方形的邊
的正方形的邊![]() 在
在![]() 軸負半軸上,點
軸負半軸上,點![]() 在第三象限內,點
在第三象限內,點![]() 的坐標為
的坐標為![]() ,經過點
,經過點![]() 的拋物線
的拋物線![]() 交
交![]() 軸于點
軸于點![]() ,其頂點為
,其頂點為![]() .
.
(1)求拋物線的解析式;
(2)若![]() 軸左側拋物線上一點
軸左側拋物線上一點![]() 關于
關于![]() 軸的對稱點
軸的對稱點![]() 恰好落在直線
恰好落在直線![]() 上,求點
上,求點![]() 的坐標;
的坐標;
(3)連接![]() ,
,![]() ,
,![]() ,請你探究在
,請你探究在![]() 軸左側的拋物線上,是否存在點
軸左側的拋物線上,是否存在點![]() ,使
,使![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,說明理由.
的坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com