
【題目】王華由![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,這些算式發現:任意兩個奇數的平方差都是8的倍數
,這些算式發現:任意兩個奇數的平方差都是8的倍數
(1)請你再寫出兩個(不同于上面算式)具有上述規律的算式;
(2)請你用含字母的代數式概括王華發現的這個規律(提示:可以使用多個字母);
(3)證明這個規律的正確性.
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B>90°,CD為∠ACB的角平分線,在AC邊上取點E,使DE=DB,且∠AED>90°.若∠A=α,∠ACB=β,則( )
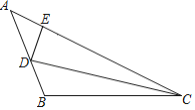
A.∠AED=180°﹣α﹣βB.∠AED=180°﹣α﹣![]() β
β
C.∠AED=90°﹣α+βD.∠AED=90°+α+![]() β
β
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線和x軸交于兩點A、B,和y軸交于點C,已知A、B兩點的橫坐標分別為﹣1,4,△ABC是直角三角形,∠ACB=90°,則此拋物線頂點的坐標為_____.
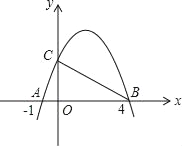
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() ,
,![]() 于點
于點![]() .
.
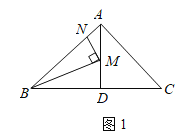
(1)如圖1所示,點![]() 分別在線段
分別在線段![]() 上,且
上,且![]() ,當
,當![]() 時,求線段
時,求線段![]() 的長;
的長;
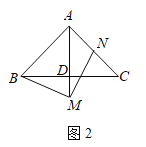
(2)如圖2,點![]() 在線段
在線段![]() 的延長線上,點
的延長線上,點![]() 在線段
在線段![]() 上,(1)中其他條件不變.
上,(1)中其他條件不變.
①線段![]() 的長為 ;
的長為 ;
②求線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D為AC上一點,且CD=CB,以BC為直徑作☉O,交BD于點E,連接CE,過D作DF![]() AB于點F,∠BCD=2∠ABD.
AB于點F,∠BCD=2∠ABD.
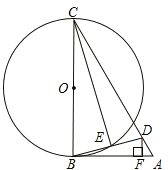
(1)求證:AB是☉O的切線;
(2)若∠A=60°,DF=![]() ,求☉O的直徑BC的長。
,求☉O的直徑BC的長。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△BAD是由△BEC在平面內繞點B旋轉60°而得,且AB⊥BC,BE=CE,連接DE.
(1)求證:△BDE≌△BCE;
(2)試判斷四邊形ABED的形狀,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
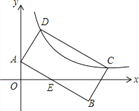
【題目】如圖,矩形ABCD中,AB=2AD,點A(0,1),點C、D在反比例函數![]() (k>0)的圖象上,AB與x軸的正半軸相交于點E,若E為AB的中點,則k的值為_____.
(k>0)的圖象上,AB與x軸的正半軸相交于點E,若E為AB的中點,則k的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于![]() 的方程
的方程![]() 有兩個不相等的實數根.
有兩個不相等的實數根.
![]() 求實數
求實數![]() 的取值范圍;
的取值范圍;
![]() 是否存在實數
是否存在實數![]() ,使方程的兩個實數根之和等于兩實數根之積的算術平方根?若存在,求出
,使方程的兩個實數根之和等于兩實數根之積的算術平方根?若存在,求出![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com