
【題目】如圖,拋物線y=ax2+c(a≠0)經過C(2,0),D(0,﹣1)兩點,并與直線y=kx交于A、B兩點,直線l過點E(0,﹣2)且平行于x軸,過A、B兩點分別作直線l的垂線,垂足分別為點M、N.

(1)求此拋物線的解析式;
(2)求證:AO=AM;
(3)探究:
①當k=0時,直線y=kx與x軸重合,求出此時![]() 的值;
的值;
②試說明無論k取何值,![]() 的值都等于同一個常數.
的值都等于同一個常數.
【答案】解:(1)y=![]() x2﹣1
x2﹣1
(2)詳見解析
(3)詳見解析
【解析】
(1)把點C、D的坐標代入拋物線解析式求出a、c,即可得解。
(2)根據拋物線解析式設出點A的坐標,然后求出AO、AM的長,即可得證。
(3)①k=0時,求出AM、BN的長,然后代入![]() 計算即可得解;
計算即可得解;
②設點A(x1,![]() x12﹣1),B(x2,
x12﹣1),B(x2,![]() x22﹣1),然后表示出
x22﹣1),然后表示出![]() ,再聯立拋物線與直線解析式,消掉未知數y得到關于x的一元二次方程,利用根與系數的關系表示出x1+x2,x12,并求出x12+x22,x12x22,然后代入進行計算即可得解。
,再聯立拋物線與直線解析式,消掉未知數y得到關于x的一元二次方程,利用根與系數的關系表示出x1+x2,x12,并求出x12+x22,x12x22,然后代入進行計算即可得解。
解:(1)∵拋物線y=ax2+c(a≠0)經過C(2,0),D(0,﹣1),
∴![]() ,解得
,解得![]() 。
。
∴拋物線的解析式為y=![]() x2﹣1。
x2﹣1。
(2)證明:設點A的坐標為(m,![]() m2﹣1),
m2﹣1),
則![]() 。
。
∵直線l過點E(0,﹣2)且平行于x軸,∴點M的縱坐標為﹣2。
∴AM=![]() m2﹣1﹣(﹣2)=
m2﹣1﹣(﹣2)=![]() m2+1。
m2+1。
∴AO=AM。
(3)①k=0時,直線y=kx與x軸重合,點A、B在x軸上,
∴AM=BN=0﹣(﹣2)=2,
∴![]() 。
。
②k取任何值時,設點A(x1,![]() x12﹣1),B(x2,
x12﹣1),B(x2,![]() x22﹣1),
x22﹣1),
則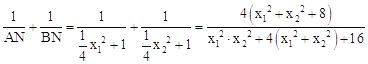 。
。
聯立,消掉y得,x2﹣4kx﹣4=0,
由根與系數的關系得,x1+x2=4k,x1x2=﹣4,
∴x12+x22=(x1+x2)2﹣2x1x2=16k2+8,x12x22=16。
∴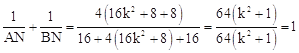 。
。
∴無論k取何值,![]() 的值都等于同一個常數1。
的值都等于同一個常數1。


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】某大型超市投入15000元資金購進![]() 、
、![]() 兩種品牌的礦泉水共600箱,礦泉水的成本價和銷售價如下表所示:
兩種品牌的礦泉水共600箱,礦泉水的成本價和銷售價如下表所示:
類別/單價 | 成本價(元/箱) | 銷售價(元/箱) |
A品牌 | 20 | 32 |
B品牌 | 35 | 50 |
(1)該大型超市購進![]() 、
、![]() 品牌礦泉水各多少箱?
品牌礦泉水各多少箱?
(2)全部銷售完600箱礦泉水,該超市共獲得多少利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】安徽某水產養殖戶去年利用“稻蝦混養”使每千克小龍蝦養殖成本降為6元,在整個銷售旺季的80天里,銷售單價P(元/千克)與時間第t(天)之間的函數關系為:P= ,日銷售量y(千克)與時間第t(天)之間的函數關系如圖所示.
,日銷售量y(千克)與時間第t(天)之間的函數關系如圖所示.
(1)求日銷售y與時間t的函數關系式?
(2)設日銷售利潤為W(元),求W與t之間的函數表達式;
(3)日銷售利潤W哪一天最大?最大利潤是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
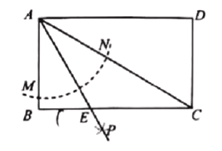
【題目】如圖,矩形![]() 以點
以點![]() 為圓心,以任意長為半徑作弧分別交
為圓心,以任意長為半徑作弧分別交![]() 、
、![]() 于
于![]() 兩點,再分別以點
兩點,再分別以點![]() 為圓心,以大于
為圓心,以大于![]() 的長為半徑作弧交于點
的長為半徑作弧交于點![]() ,作射線
,作射線![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,則矩形
,則矩形![]() 的面積等于__________.
的面積等于__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在四邊形ABCD中,對角線AC與BD相交于點O,![]() ,下列判斷中錯誤的是( )
,下列判斷中錯誤的是( )
A.如果![]() ,
,![]() ,那么四邊形ABCD是平行四邊形
,那么四邊形ABCD是平行四邊形
B.如果![]() ,
,![]() ,那么四邊形ABCD是矩形
,那么四邊形ABCD是矩形
C.如果![]() ,
,![]() ,那么四邊形ABCD是菱形
,那么四邊形ABCD是菱形
D.如果![]() ,AC垂直平分BD,那么四邊形ABCD是正方形
,AC垂直平分BD,那么四邊形ABCD是正方形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】據調查,超速行駛是引發交通事故的主要原因之一,所以規定以下情境中的速度不得超過15m/s在一條筆直公路BD的上方A處有一探測儀,如平面幾何圖,AD=24m,∠D=90°,第一次探測到一輛轎車從B點勻速向D點行駛,測得∠ABD=31°,2秒后到達C點,測得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,結果精確到1m).
(1)求B,C的距離.
(2)通過計算,判斷此轎車是否超速.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末,小華和小亮想用所學的數學知識測量家門前小河的寬.測量時,他們選擇了河對岸邊的一棵大樹,將其底部作為點A,在他們所在的岸邊選擇了點B,使得AB與河岸垂直,并在B點豎起標桿BC,再在AB的延長線上選擇點D豎起標桿DE,使得點E與點C、A共線.
已知:CB⊥AD,ED⊥AD,測得BC=1m,DE=1.5m,BD=8.5m.測量示意圖如圖所示.請根據相關測量信息,求河寬AB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個工程隊分別同時開挖兩段河渠,所挖河渠的長度y(m)與挖掘時間x(h)之間的關系如圖所示,請根據圖象所提供的信息解答下列問題:

(1)乙隊開挖到30m時,用了_____ h. 開挖6h時甲隊比乙隊多挖了____ m;
(2)請你求出:
①甲隊在![]() 的時段內,y與x之間的函數關系式;
的時段內,y與x之間的函數關系式;
②乙隊在![]() 的時段內,y與x之間的函數關系式;
的時段內,y與x之間的函數關系式;
(3)當x 為何值時,甲、 乙兩隊在 施工過程中所挖河渠的長度相等?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com