
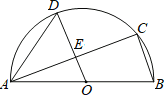
【題目】如圖,AB是半圓O的直徑,C、D是半圓O上的兩點,且OD∥BC,OD與AC交于點E.
(1)若∠B=70°,求∠CAD的度數;
(2)若AB=10,AC=8,求DE的長.
【答案】(1)35°;(2)2
【解析】
(1)由AB是半圓O的直徑,根據直徑所對的圓周角是直角,可得∠C=90°,又由OD∥BC,可求得∠AEO的度數,然后求得∠CAB的度數,繼而求得答案;
(2)由勾股定理,首先求得BC的長,然后由三角形中位線的性質,求得OE的長,繼而求得答案.
(1)∵AB是半圓O的直徑,
∴∠ACB=90°,
又∵OD∥BC,
∴∠AEO=90°,
即OE⊥AC,∠CAB=90°﹣∠B=90°﹣70°=20°.
∵OA=OD,
∴∠DAO=∠ADO=![]() (180﹣70)°=55°,
(180﹣70)°=55°,
∴∠CAD=∠DAO﹣∠CAB=55°﹣20°=35°;
(2)在直角△ABC中,BC=![]() =6.
=6.
∵OE⊥AC,
∴AE=EC=4,
又∵OA=OB,
∴OE=![]() BC=3,
BC=3,
又∵OD=![]() AB=5,
AB=5,
∴DE=OD-OE=5-![]() =2.
=2.


科目:初中數學 來源: 題型:
【題目】小峰和小軒用兩枚質地均勻的骰子做游戲,規則如下:每人隨機擲兩枚骰子一次(若擲出的兩枚骰子摞在一起,則重擲),點數和大的獲勝;點數和相同為平局.
依據上述規則,解答下列問題:
(1)隨機擲兩枚骰子一次,用列表法或樹狀圖法求點數和為10的概率;
(2)小峰先隨機擲兩枚骰子一次,點數和是10,求小軒隨機擲兩枚骰子一次,勝小峰的概率.(骰子:六個面分別有1、2、3、4、5、6個小圓點的立方塊.點數和:兩枚骰子朝上的點數之和.)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 己知拋物線![]() 向右平移2個單位,再向下平移3個單位后恰好經過點
向右平移2個單位,再向下平移3個單位后恰好經過點![]() .
.
(1)求平移后拋物線的解析式;
(2)點A在平移后物線上,點A在該拋物線對稱軸的右側,將點A繞著原點逆時針旋轉90°得到點B,設點A的橫坐標為t;
①用t表示點B的坐標;
②若直線![]() ,且
,且![]() 與平移后拋物線只有一個交點C,當點
與平移后拋物線只有一個交點C,當點![]() 到直線AC距離取得最大值時,此時直線AC解析式.
到直線AC距離取得最大值時,此時直線AC解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于以AB為直徑的⊙O,過點A作⊙O的切線,與BC的延長線相交于點D,在CB上截取CE=CD,連接AE并延長,交⊙O于點F,連接CF.
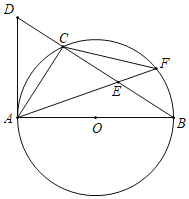
(1)求證:AC=CF;
(2)若AB=4,sinB![]() ,求EF的長.
,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=﹣x2+bx+c上部分點的橫坐標x,縱坐標y的對應值如下表:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
從上表可知,下列說法正確的個數是( )
①拋物線與x軸的一個交點為(﹣2,0);
②拋物線與y軸的交點為(0,6);
③拋物線的對稱軸是x=1;
④在對稱軸左側y隨x增大而減小;
⑤當y>0,則x的取值范圍是-2<x<3
A.①②③B.②③④C.②④⑤D.①②⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
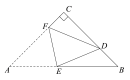
【題目】如圖,在△ABC中,AC=BC=4![]() ,∠C=90°,點D在BC上,且CD=3DB,將△ABC折疊,使點A與點D重合,EF為折痕,則tan∠BED的值是_____.
,∠C=90°,點D在BC上,且CD=3DB,將△ABC折疊,使點A與點D重合,EF為折痕,則tan∠BED的值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在四邊形ABCD中,AB∥CD,∠B=90°,AB=2CD.動點P從點A出發,在四邊形ABCD的邊上沿A→B→C的方向以1cm/s的速度勻速移動,到達點C時停止移動。已知△APD的面積S(cm 2)與點P運動的時間t(s)之間的函數圖象如圖②所示,根據題意解答下列問題
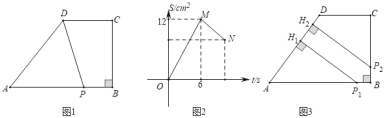
(1)在圖①中,AB= cm, BC= cm.
(2)求圖2中線段MN的函數關系式(并寫出t的取值范圍) .
(3)如圖③,設動點P用了t1 (s)到達點P1處,用了t2 (s)到達點P2處,分別過P1、P2作AD的垂線,垂足為H1、H2.當P1H1= P2H2=4時,連P1P2,求△BP1P2的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
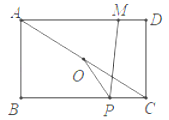
【題目】如圖,在矩形ABCD中,AB=4,AD=5,連接AC,O是AC的中點,M是AD上一點,且MD=1,P是BC上一動點,則PM﹣PO的最大值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在正方形ABCD中,點E在邊CD上,AQ⊥BE于點Q,DP⊥AQ于點P.
(1)求證:AP=BQ;
(2)在不添加任何輔助線的情況下,請直接寫出圖中四對線段,使每對中較長線段與較短線段長度的差等于PQ的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com