
【題目】在矩形紙片![]() 中,
中,![]() 是邊
是邊![]() 上的點,將紙片沿
上的點,將紙片沿![]() 折疊,使點
折疊,使點![]() 落在點
落在點![]() 處,連接
處,連接![]() ,當
,當![]() 為直角三角形時,
為直角三角形時,![]() 的長為___________.
的長為___________.
【答案】3或6.
【解析】
試題分析:由AD=8、AB=6結合矩形的性質可得出AC=10,△EFC為直角三角形分兩種情況:①當∠EFC=90°時,可得出AE平分∠BAC,根據角平分線的性質即可得出![]() ,解之即可得出BE的長度;②當∠FEC=90°時,可得出四邊形ABEF為正方形,根據正方形的性質即可得出BE的長度.
,解之即可得出BE的長度;②當∠FEC=90°時,可得出四邊形ABEF為正方形,根據正方形的性質即可得出BE的長度.
∵AD=8,AB=6,四邊形ABCD為矩形,
∴BC=AD=8,∠B=90°,∴AC=![]() =10.
=10.
△EFC為直角三角形分兩種情況:
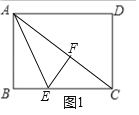
①當∠EFC=90°時,如圖1所示.
∵∠AFE=∠B=90°,∠EFC=90°,∴點F在對角線AC上,
∴AE平分∠BAC,∴![]() ,即
,即![]() ,∴BE=3;
,∴BE=3;
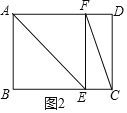
②當∠FEC=90°時,如圖2所示.
∵∠FEC=90°,∴∠FEB=90°,∴∠AEF=∠BEA=45°,
∴四邊形ABEF為正方形,∴BE=AB=6.
綜上所述:BE的長為3或6.
故答案為:3或6.


科目:初中數學 來源: 題型:
【題目】某籃球隊12名隊員的年齡如下表所示:
年齡(歲) | 18 | 19 | 20 | 21 |
人數 | 5 | 4 | 1 | 2 |
則這12名隊員年齡的眾數和中位數分別是( )
A.18,19B.18,19.5C.5,4D.5, 4.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某地區的電力資源豐富,并且得到了較好的開發。該地區一家供電公司為了鼓勵居民用電,采用分段計費的方法來計算電費. 月用電量x(度)與相應電費y(元)之間的函數圖像如圖所示.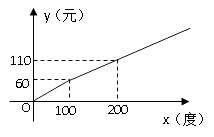
(1)月用電量為100度時,應交電費元;
(2)當x≥100時,求y與x之間的函數關系式;
(3)月用電量為260度時,應交電費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了進一步了解某校八年級學生的身體素質情況,體育老師對該校八年級(1)班50位學生進行一分鐘跳繩次數測試,以測試數據為樣本,繪制出部分頻數分布表和部分頻數分布直方圖,圖表如下所示:
組別 | 次數x | 頻數(人數) |
第1組 | 80≤x<100 | 6 |
第2組 | 100≤x<120 | 8 |
第3組 | 120≤x<140 | a |
第4組 | 140≤x<160 | 18 |
第5組 | 160≤x<180 | 6 |
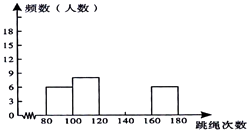
請結合圖表完成下列問題:
(1)求表中a的值;
(2)請把頻數分布直方圖補充完整;
(3)若在一分鐘內跳繩次數少于120次的為測試不合格,則該校八年級共1000人中,一分鐘跳繩
不合格的人數大約有多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=1cm,AD=3cm,點Q從A點出發,以1cm/s的速度沿AD向終點D運動,點P從點C出發,以1cm/s的速度沿CB向終點B運動,當這兩點中有一點到達自己的終點時,另一點也停止運動,兩點同時出發,運動了t秒.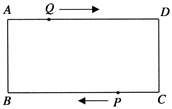
(1)當0<t<3,判斷四邊形BQDP的形狀,并說明理由;
(2)求四邊形BQDP的面積S與運動時間t的函數關系式;
(3)求當t為何值時,四邊形BQDP為菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l1的函數解析式為y=﹣2x+4,且l1與x軸交于點D,直線l2經過點A、B,直線l1、l2交于點C.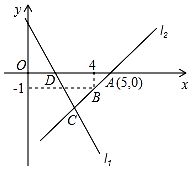
(1)求直線l2的函數解析式;
(2)求△ADC的面積;
(3)在直線l2上是否存在點P,使得△ADP面積是△ADC面積的2倍?如果存在,請求出P坐標;如果不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com